Now for a more involved PRISM case study: a model of the EGL contract signing protocol of Even, Goldreich & Lempel. The PRISM code is shown below.
// Randomised protocol for signing contracts taken from: // S. Even, O. Goldreich, and A. Lempel. // A randomized protocol for signing contracts. // Communications of the ACM, 28(6):637 647, 1985. //----------------------------------------------------------------------------------------- dtmc // Model is a DTMC (no nondeterminism) // CONSTANTS: // N: number of pairs of secrets each party sends const int N; // L: number of bits in each secret (fix at 2) const int L=2; // FORMULAE: // B knows a pair of secrets formula kB = ( (a1_0=L & a2_0=L) | (a1_1=L & a2_1=L) | (a1_2=L & a2_2=L) | (a1_3=L & a2_3=L) | (a1_4=L & a2_4=L) | (a1_5=L & a2_5=L) | (a1_6=L & a2_6=L) | (a1_7=L & a2_7=L) | (a1_8=L & a2_8=L) | (a1_9=L & a2_9=L)); // A knows a pair of secrets formula kA = ( (b1_0=L & b2_0=L) | (b1_1=L & b2_1=L) | (b1_2=L & b2_2=L) | (b1_3=L & b2_3=L) | (b1_4=L & b2_4=L) | (b1_5=L & b2_5=L) | (b1_6=L & b2_6=L) | (b1_7=L & b2_7=L) | (b1_8=L & b2_8=L) | (b1_9=L & b2_9=L)); //----------------------------------------------------------------------------------------- // Scheduler: used to order the sending of messages between parties A and B module scheduler // b: which bit of the secret a party should send next b : [1..L]; // n: which secret a party should send next n : [0..max(N-1,1)]; // phase: current phase of the protocol // 1 = sending messages of the form OT(.,.,.,.) // 2&3 = sending secrets 1..N and N+1..2N, respectively // 4 = finished phase : [1..5]; // party: which party moves next party : [1..2]; // FIRST PHASE: // A sends a message, B will go next [receiveB] phase=1 & party=1 -> (party'=2); // B sends a message, move onto next message and go back to A [receiveA] phase=1 & party=2 & n<N-1 -> (party'=1) & (n'=n+1); // B sends final (Nth) message, move to next phase [receiveA] phase=1 & party=2 & n=N-1 -> (party'=1) & (phase'=2) & (n'=0); // SECOND AND THIRD PHASES (interleaved for A and B): // A sends bth bit of nth secret (for n=1..N-1), move to next secret [receiveB] phase=2 & party=1 & n<N-1-> (n'=n+1); // A sends bth bit of Nth secret, move to next phase (N+1..2N) [receiveB] phase=2 & party=1 & n=N-1 -> (phase'=3) & (n'=0); // A sends bth bit of (N+n)th secret (for n=1..N-1), move to next secret [receiveB] phase=3 & party=1 & n<N-1-> (n'=n+1); // A sends bth bit of last (2Nth) secret, B will go next [receiveB] phase=3 & party=1 & n=N-1 -> (phase'=2) & (party'=2) & (n'=0); // B sends bth bit of nth secret (for n=1..N-1), move to next secret [receiveA] phase=2 & party=2 & n<N-1 -> (n'=n+1); // B sends bth bit of Nth secret, move to next phase (N+1..2N) [receiveA] phase=2 & party=2 & n=N-1 -> (phase'=3) & (n'=0); // B sends bth bit of (N+n)th secret (for n=1..N-1), move to next secret [receiveA] phase=3 & party=2 & n<N-1 -> (n'=n+1); // B sends bth bit of last (2Nth) secret, increment b and go back to A [receiveA] phase=3 & party=2 & n=N-1 & b<L -> (phase'=2) & (party'=1) & (n'=0) & (b'=b+1); // B sends final (Lth) bit of last (2Nth) secret, protocol is now finished [receiveA] phase=3 & party=2 & n=N-1 & b=L -> (phase'=4); // FINISHED (loop) [] phase=4 -> (phase'=4); endmodule //----------------------------------------------------------------------------------------- // Party A module partyA // How many bits of each of B's secrets A currently knows // Secrets are in pairs and thus divided into two sets. // b1_i stores the value (number of bits known) for the ith secret // of the first set of secrets. b2_i stores the value // for the ith secret of the second set of secrets. // (Technical note: Keep pairs of secrets together // to give a more structured model and hence smaller MTBDD) b1_0 : [0..L]; b2_0 : [0..L]; b1_1 : [0..L]; b2_1 : [0..L]; b1_2 : [0..L]; b2_2 : [0..L]; b1_3 : [0..L]; b2_3 : [0..L]; b1_4 : [0..L]; b2_4 : [0..L]; b1_5 : [0..L]; b2_5 : [0..L]; b1_6 : [0..L]; b2_6 : [0..L]; b1_7 : [0..L]; b2_7 : [0..L]; b1_8 : [0..L]; b2_8 : [0..L]; b1_9 : [0..L]; b2_9 : [0..L]; // A receives either secret n-1 or N+(n-1) with equal probability // (using Oblivious Transfer (OT) protocol) // Note: get full secret here, i.e. all L bits [receiveA] phase=1 & n=0 -> 0.5 : (b1_0'=L) + 0.5 : (b2_0'=L); [receiveA] phase=1 & n=1 -> 0.5 : (b1_1'=L) + 0.5 : (b2_1'=L); [receiveA] phase=1 & n=2 -> 0.5 : (b1_2'=L) + 0.5 : (b2_2'=L); [receiveA] phase=1 & n=3 -> 0.5 : (b1_3'=L) + 0.5 : (b2_3'=L); [receiveA] phase=1 & n=4 -> 0.5 : (b1_4'=L) + 0.5 : (b2_4'=L); [receiveA] phase=1 & n=5 -> 0.5 : (b1_5'=L) + 0.5 : (b2_5'=L); [receiveA] phase=1 & n=6 -> 0.5 : (b1_6'=L) + 0.5 : (b2_6'=L); [receiveA] phase=1 & n=7 -> 0.5 : (b1_7'=L) + 0.5 : (b2_7'=L); [receiveA] phase=1 & n=8 -> 0.5 : (b1_8'=L) + 0.5 : (b2_8'=L); [receiveA] phase=1 & n=9 -> 0.5 : (b1_9'=L) + 0.5 : (b2_9'=L); // A receives single bit for secrets 0..N-1 (when scheduler module in phase 2) [receiveA] phase=2 & n=0 -> (b1_0'=min(b1_0+1,L)); [receiveA] phase=2 & n=1 -> (b1_1'=min(b1_1+1,L)); [receiveA] phase=2 & n=2 -> (b1_2'=min(b1_2+1,L)); [receiveA] phase=2 & n=3 -> (b1_3'=min(b1_3+1,L)); [receiveA] phase=2 & n=4 -> (b1_4'=min(b1_4+1,L)); [receiveA] phase=2 & n=5 -> (b1_5'=min(b1_5+1,L)); [receiveA] phase=2 & n=6 -> (b1_6'=min(b1_6+1,L)); [receiveA] phase=2 & n=7 -> (b1_7'=min(b1_7+1,L)); [receiveA] phase=2 & n=8 -> (b1_8'=min(b1_8+1,L)); [receiveA] phase=2 & n=9 -> (b1_9'=min(b1_9+1,L)); // A receives single bits for secrets N..2N-1 (when scheduler module in phase 3) [receiveA] phase=3 & n=0 -> (b2_0'=min(b2_0+1,L)); [receiveA] phase=3 & n=1 -> (b2_1'=min(b2_1+1,L)); [receiveA] phase=3 & n=2 -> (b2_2'=min(b2_2+1,L)); [receiveA] phase=3 & n=3 -> (b2_3'=min(b2_3+1,L)); [receiveA] phase=3 & n=4 -> (b2_4'=min(b2_4+1,L)); [receiveA] phase=3 & n=5 -> (b2_5'=min(b2_5+1,L)); [receiveA] phase=3 & n=6 -> (b2_6'=min(b2_6+1,L)); [receiveA] phase=3 & n=7 -> (b2_7'=min(b2_7+1,L)); [receiveA] phase=3 & n=8 -> (b2_8'=min(b2_8+1,L)); [receiveA] phase=3 & n=9 -> (b2_9'=min(b2_9+1,L)); endmodule //----------------------------------------------------------------------------------------- // Construct module for party B through renaming module partyB=partyA[b1_0=a1_0 ,b1_1=a1_1 ,b1_2=a1_2 ,b1_3=a1_3 ,b1_4=a1_4 ,b1_5=a1_5 ,b1_6=a1_6 ,b1_7=a1_7 ,b1_8=a1_8 ,b1_9=a1_9, b2_0=a2_0 ,b2_1=a2_1 ,b2_2=a2_2 ,b2_3=a2_3 ,b2_4=a2_4 ,b2_5=a2_5 ,b2_6=a2_6 ,b2_7=a2_7 ,b2_8=a2_8 ,b2_9=a2_9, receiveA=receiveB] endmodule
 The first step is to understand how the algorithm works
(look at these slides)
and then work out how the algorithm is represented by the PRISM model shown above.
The following notes should help.
The first step is to understand how the algorithm works
(look at these slides)
and then work out how the algorithm is represented by the PRISM model shown above.
The following notes should help.
The PRISM model comprises three modules. Two of these represent the (symmetric) parties, A and B, which take part in the contract signing. The third represents a scheduler which controls the order in which A and B send messages to each other, and thus captures the details of the algorithm itself.
Let's look first at the scheduler module. It has 4 variables which are used to keep track of the current state of execution of the algorithm. The purpose of each is explained in the comments in the file. The commands below this show how these variables are updated at each step, depending on their current value, for each phase of the algorithm. Again the comments before each line of the file describe the correspondence between the algorithm and the PRISM model.
The scheduler module controls the behaviour of each party by synchronising with them. Note the labels receiveA and receiveB at the start of the commands in the scheduler module (and also in the corresponding party modules). This means that at each step, one of the parties (A or B) will simultaneously update as the scheduler does.
The module for party A keeps track of the number of bits of each secret of B's that A has received from B (and vice versa for the module representing party B). The code above can be used for the case with N=10 pairs of secrets. In fact, it can also be used for any value of N less than 10. In these cases, we only actually use the variables b1_i and b2_i for i<N.
 Download the model egl.pm from above and load it into PRISM.
Check for the green tick indicating that model has loaded and parsed correctly.
Download the model egl.pm from above and load it into PRISM.
Check for the green tick indicating that model has loaded and parsed correctly.
 Using a fairly small value of N (say 4),
generate a random path through the model using the simulator.
You should find that the path stops after about 40 steps
(when the contract signing algorithm ends).
Look at the values of the first 4 variables
in the table representing the path.
Check that this matches your understanding of how the algorithm works.
Using a fairly small value of N (say 4),
generate a random path through the model using the simulator.
You should find that the path stops after about 40 steps
(when the contract signing algorithm ends).
Look at the values of the first 4 variables
in the table representing the path.
Check that this matches your understanding of how the algorithm works.
 Load the following properties file into PRISM:
Load the following properties file into PRISM:
// Party B knows a pair of A's secrets (i.e. has // all L bits for at least one of the secrets) label "knowB" = ( (a1_0=L & a2_0=L) | (a1_1=L & a2_1=L) | (a1_2=L & a2_2=L) | (a1_3=L & a2_3=L) | (a1_4=L & a2_4=L) | (a1_5=L & a2_5=L) | (a1_6=L & a2_6=L) | (a1_7=L & a2_7=L) | (a1_8=L & a2_8=L) | (a1_9=L & a2_9=L)); // Party A knows a pair of B's secrets (i.e. has // all L bits for at least one of the secrets) label "knowA" = ( (b1_0=L & b2_0=L) | (b1_1=L & b2_1=L) | (b1_2=L & b2_2=L) | (b1_3=L & b2_3=L) | (b1_4=L & b2_4=L) | (b1_5=L & b2_5=L) | (b1_6=L & b2_6=L) | (b1_7=L & b2_7=L) | (b1_8=L & b2_8=L) | (b1_9=L & b2_9=L)); // What is the probability (from the initial state) // of reaching a state where B knows a pair and A does not? P=?[ true U !"knowA" & "knowB" ] // What is the probability (from the initial state) // of reaching a state where B knows a pair and A does not? P=?[ true U "knowA" & !"knowB" ]
 Study the properties file above.
There are two labels, used to identify certain important states of the model,
and then two properties.
The first property gives the probability, from the initial state of the model,
of reaching a state where B knows a pair of A's secrets and A does not know one of B's.
This is a measure of how likely the algorithm is to be unfair towards party A.
The second property is the same, but with two parties reversed.
Study the properties file above.
There are two labels, used to identify certain important states of the model,
and then two properties.
The first property gives the probability, from the initial state of the model,
of reaching a state where B knows a pair of A's secrets and A does not know one of B's.
This is a measure of how likely the algorithm is to be unfair towards party A.
The second property is the same, but with two parties reversed.
 At this point, you should modify some of the settings in PRISM.
This will make verification much more efficient on this example.
Launch the "Options" dialog from the main menu.
Firstly, change the "engine" from "hybrid" to "MTBDD".
Secondly, change the "use precomputation" option from "yes" to "no".
At this point, you should modify some of the settings in PRISM.
This will make verification much more efficient on this example.
Launch the "Options" dialog from the main menu.
Firstly, change the "engine" from "hybrid" to "MTBDD".
Secondly, change the "use precomputation" option from "yes" to "no".
 Plot the results of the first property for N=1..10.
Plot the results for the second property for the same range on the same graph.
Plot the results of the first property for N=1..10.
Plot the results for the second property for the same range on the same graph.
The graph should look something like this:
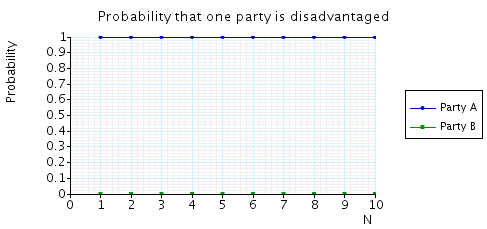
The interpretation is that, for any value of N, with probability 1, party B eventually knows a pair of secrets when A does not.
We will now model an improved version of the algorithm. We only need to change the scheduler module and, more specifically, only the commands which control the second and third phases of the algorithm.
 Save a new copy the model file as egl2.pm and then modify this new file,
replacing this code in the original model:
Save a new copy the model file as egl2.pm and then modify this new file,
replacing this code in the original model:
// SECOND AND THIRD PHASES (interleaved for A and B): // A sends bth bit of nth secret (for n=1..N-1), move to next secret [receiveB] phase=2 & party=1 & n<N-1-> (n'=n+1); // A sends bth bit of Nth secret, move to next phase (N+1..2N) [receiveB] phase=2 & party=1 & n=N-1 -> (phase'=3) & (n'=0); // A sends bth bit of (N+n)th secret (for n=1..N-1), move to next secret [receiveB] phase=3 & party=1 & n<N-1-> (n'=n+1); // A sends bth bit of last (2Nth) secret, B will go next [receiveB] phase=3 & party=1 & n=N-1 -> (phase'=2) & (party'=2) & (n'=0); // B sends bth bit of nth secret (for n=1..N-1), move to next secret [receiveA] phase=2 & party=2 & n<N-1 -> (n'=n+1); // B sends bth bit of Nth secret, move to next phase (N+1..2N) [receiveA] phase=2 & party=2 & n=N-1 -> (phase'=3) & (n'=0); // B sends bth bit of (N+n)th secret (for n=1..N-1), move to next secret [receiveA] phase=3 & party=2 & n<N-1 -> (n'=n+1); // B sends bth bit of last (2Nth) secret, increment b and go back to A [receiveA] phase=3 & party=2 & n=N-1 & b<L -> (phase'=2) & (party'=1) & (n'=0) & (b'=b+1); // B sends final (Lth) bit of last (2Nth) secret, protocl is now finished [receiveA] phase=3 & party=2 & n=N-1 & b=L -> (phase'=4);
with this code:
// SECOND AND THIRD PHASES (interleaved for A and B): // A sends bth bit of nth secret (for n=1..N-1), move to next secret [receiveB] phase=2 & party=1 & n<N-1-> (n'=n+1); // A sends bth bit of Nth secret, B will go next [receiveB] phase=2 & party=1 & n=N-1 -> (phase'=2) & (party'=2) & (n'=0); // B sends bth bit of nth secret (for n=1..N-1), move to next secret [receiveA] phase=2 & party=2 & n<N-1 -> (n'=n+1); // B sends bth bit of Nth secret, move to next phase (N+1..2N) and back to A [receiveA] phase=2 & party=2 & n=N-1 -> (phase'=3) & (party'=1) & (n'=0); // A sends bth bit of (N+n)th secret (for n=1..N-1), move to next secret [receiveB] phase=3 & party=1 & n<N-1-> (n'=n+1); // A sends bth bit of last (2Nth) secret, B will go next [receiveB] phase=3 & party=1 & n=N-1 -> (phase'=3) & (party'=2) & (n'=0); // B sends bth bit of (N+n)th secret (for n=1..N-1), move to next secret [receiveA] phase=3 & party=2 & n<N-1 -> (n'=n+1); // B sends bth bit of last (2Nth) secret, increment b and go back to A [receiveA] phase=3 & party=2 & n=N-1 & b<L -> (phase'=2) & (party'=1) & (n'=0) & (b'=b+1); // B sends final (Lth) bit of last (2Nth) secret, protocol is now finished [receiveA] phase=3 & party=2 & n=N-1 & b=L -> (phase'=4);
 Now reload the property file egl.pctl used before
and plot the results for the first property for the same range of N (1..10) on the same graph.
Do the same for the second property.
You should get something like this:
Now reload the property file egl.pctl used before
and plot the results for the first property for the same range of N (1..10) on the same graph.
Do the same for the second property.
You should get something like this:
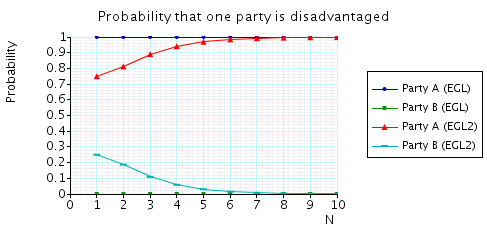
We see that, for small values of N, the improved algorithm (EGL2) is better, i.e. less likely to be unfair to party A. For larger values of N, however, there is very little improvement.
 Save your graph (export as a "PRISM graph").
This will allow you to reload it and add to it later.
Save your graph (export as a "PRISM graph").
This will allow you to reload it and add to it later.
 Look at the other 2 versions of the algorithm, EGL3 and EGL4,
as described in the slides mentioned above.
Create two new model files, egl3.pm and egl4.pm which model these versions in PRISM.
As for modelling EGL2 above, you only need to change one part of the file,
corresponding to phases 2 and 3 of the scheduler module.
Some tips:
Look at the other 2 versions of the algorithm, EGL3 and EGL4,
as described in the slides mentioned above.
Create two new model files, egl3.pm and egl4.pm which model these versions in PRISM.
As for modelling EGL2 above, you only need to change one part of the file,
corresponding to phases 2 and 3 of the scheduler module.
Some tips:
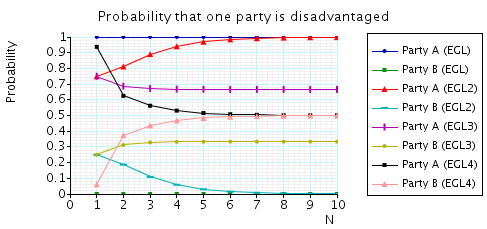
There are several other properties which can be investigated for these algorithms. These use the costs and rewards capabilities of PRISM (see here and here).
 Have a look at
this part
of the web page for this case study on the PRISM web site.
By adding the appropriate reward structure to your models,
and creating a new property, analyse
"the expected number of messages from B that A needs to knows a pair once B knows a pair".
You should be able to recreate (at least the first 4 plots) from the graph on this web page.
Have a look at
this part
of the web page for this case study on the PRISM web site.
By adding the appropriate reward structure to your models,
and creating a new property, analyse
"the expected number of messages from B that A needs to knows a pair once B knows a pair".
You should be able to recreate (at least the first 4 plots) from the graph on this web page.
[ Back to index ]