Power Management is an important area of research due to an increasing trend in the usage of portable, mobile and hand-held electronic devices. These devices usually run on batteries and any savings in power usage translate to extended battery life. Various approaches to low power design have been explored, at device, circuit and micro-architecture level. System level power management exploits application characteristics and manages various system devices for power optimization. System components such as network interface cards, disk drives and DRAM are manufactured with a number of power modes which can be changed by an operating system through standard APIs such as ACPI. However, in order to take advantage of these power modes and APIs, the power management strategies need to be implemented at the O/S level. In this context, Dynamic Power Management (DPM) refers to strategies that attempt to make power mode changing decisions based on the information about their usage pattern available at runtime. The objective is to minimize power consumption, while minimizing the effect on performance.
Stochastic modelling based approaches to DPM have considered stationary discrete-time Markov chains [PBBM98], continuous-time Markov chains [QP99] or their variants [SBM99]. The approach models the input arrival process and the behaviour of the power managed components. This is done by creating stochastic matrices or generator matrices for these processes, and then formulating optimization problems whose solution is the required strategy.
Power management in embedded computing systems is achieved by actively changing the power consumption profile of the system by putting its components into power/energy states which are sufficient to meet functionality requirements. For example, an idling component (such as a disk drive) can be put into a slow-down or shutdown state. Of course, bringing such a component into an active state may then require additional energy and/or latency to service the tasks. The DPM problem can be defined as follows:
Given a power managed component, such as a disk drive or a network interface card, derive a randomized power management strategy which minimizes average power dissipation, under the constraint that the average delay suffered by requests coming for service by the component is bounded by an a priori constant.
Dynamic Power Management (DPM) attempts to make optimal decisions (usually under the control of the operating system) at runtime based on dynamically changing system state, functionality and delay requirements. A survey of the DPM techniques can be found in [BBM00]. DPM strategies are classified into two main groups: predictive schemes and stochastic optimum control schemes.
Predictive schemes attempt to predict the timing of future input to the system and, based on such predictions, schedule shutdown (usually to a single lower power state) of the system.
Stochastic optimum control schemes involve the construction (and validation) of a mathematical model of the system that lends itself to the formulation of a stochastic optimization problem, and then creation of system power profile strategies which achieve the highest power savings in the presence of the uncertainty related to system inputs.
Stochastic control oriented dynamic power management work relies on modelling inter-arrival times using an exponential distribution. In practice, such stochastic modelling seems to work well for specific kinds of applications. However, the approaches vary in the modelling of time. For example, in [BBPM99] the arrival process and service process are both modelled as discrete time Markov chains, whereas in [QP99] they are modelled as continuous time Markov chains. In more recent work, such as in [SBM99], extended models which incorporate more general stochastic processes for modelling event arrivals have been considered.
In each of the case studies we consider, the system model has the following form.
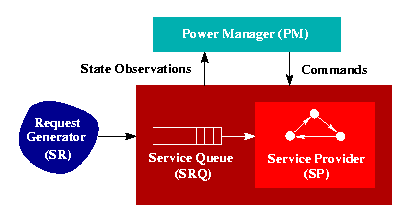
The model consists of a Service Requester (SR), a Service Provider (SP), a Service Request Queue (SRQ), and the power manager (PM). The SR models the arrival of requests and the SRQ corresponds to a (finite) queue in which the requests that cannot immediately be served are stored. The SP is the resource which services requests. It can have several states of operation with varying service rates (the time taken to service requests). The PM is a controller that observes the system and issues commands to the SP which correspond instruct it to change its current state.
For each case study, we have designed generic models of the the system in PRISM's input description language. Then, using PRISM, we are able to construct the full generator matrix of a system, and hence construct the optimization problem whose solution is the optimal policy. Moreover, once the optimal policy is found, by using the generic description we can construct a model of the system corresponding to this policy and investigate its performance, varying the number of requests awaiting service to obtain different stochastic policies. The calculation is performed by generating the matrices in PRISM and formulating and solving the linear optimization problem in MAPLE.
The PRISM representation consists of a number of modules representing the different components of the system, namely the PM, SP, SR and SRQ. Therefore, to represent different stochastic strategies one needs only to modify the PM module.
Using this approach we have considered the following case studies: