This example concerns a mail delivery robot. It is a simple example to show how PRISM can be used to verify the design of a robot system.
A workplace is equipped with a robot for internal mail delivery. From each office, workers can call the robot whenever they have mail to send. When the robot arrives, it collects the mail and the number of the office to which it should be delivered. The robot has its own "office" where it can recharge its battery. If its battery is empty, the robot stops working.
In the first part, the robot uses a completely random pattern similar to those of vacuum cleaning robots, so the model is a Discrete-Time Markov Chain (DTMC). In the second part, the movement of the robot is left unspecified, and thus the model is a Markov Decision Process (MDP). We will use PRISM to synthesise optimal strategies for this robot.
The robot contains several components:
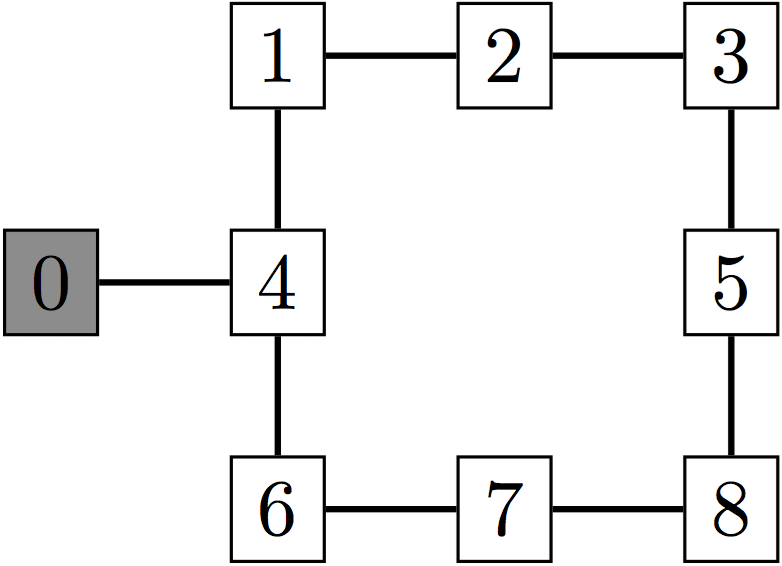
A map of the workplace is depicted below. Offices are labelled from 1 to 8. Office 0 is where the robot recharges its battery. Lines represent the corridors the robot can use to navigate between offices.
The initial PRISM model is the following:
dtmc // Maximal charge of the robot battery counted as the number of moves. const int batteryCharge=20 ; // Speed at which the battery recharges as the number of moves per unit of time. const int chargeSpeed = 4; // Frequency at which new delivery requests arrive. const double f = 0.5; //------------------------------------------------------------------------------ // Controller of robot movements module controller p: [0..8] init 0; [move] p=0&c>0 -> 1/2:(p'=0) + 1/2:(p'=4); [move] p=4&c>0 -> 1/4:(p'=0) + 1/4:(p'=1) + 1/4:(p'=4) + 1/4:(p'=6); [move] p=1&c>0 -> 1/3:(p'=4) + 1/3:(p'=1) + 1/3:(p'=2); [move] p=2&c>0 -> 1/3:(p'=1) + 1/3:(p'=2) + 1/3:(p'=3); [move] p=3&c>0 -> 1/3:(p'=2) + 1/3:(p'=3) + 1/3:(p'=5); [move] p=5&c>0 -> 1/3:(p'=3) + 1/3:(p'=5) + 1/3:(p'=8); [move] p=6&c>0 -> 1/3:(p'=4) + 1/3:(p'=6) + 1/3:(p'=7); [move] p=7&c>0 -> 1/3:(p'=6) + 1/3:(p'=7) + 1/3:(p'=8); [move] p=8&c>0 -> 1/3:(p'=5) + 1/3:(p'=7) + 1/3:(p'=8); // When the battery is empty, loop over current state. [] c=0 -> 1.0 : true; endmodule //------------------------------------------------------------------------------ // Charge of the battery module battery c: [0..batteryCharge] init batteryCharge; // When position is equal to 0, recharge the battery. [move] c<=batteryCharge-chargeSpeed & p=0 -> 1.0 : (c'=c+chargeSpeed); [move] c> batteryCharge-chargeSpeed & p=0 -> 1.0 : (c'=batteryCharge); // Otherwise discharge it. [move] c>0 & p!=0 -> 1.0 : (c'=c-1); endmodule //------------------------------------------------------------------------------ // Handling of tasks and task completion module task fd:[0..2] init 0; // 0 no task // 1 fetch mail // 2 deliver mail g: [1..8] init 1; // Location to reach in order to complete the current task. // Randomly choose a new task with probability f. [move] fd=0 -> f/8:(g'=1)&(fd'=1) + f/8:(g'=2)&(fd'=1) + f/8:(g'=3)&(fd'=1) + f/8:(g'=4)&(fd'=1) + f/8:(g'=5)&(fd'=1) + f/8:(g'=6)&(fd'=1) + f/8:(g'=7)&(fd'=1) + f/8:(g'=8)&(fd'=1) + 1-f:true; [move] fd>0 & g!=p -> 1.0:true; // The robot reaches a location where it fetches mail, then // randomly chooses destination. [] g=p & fd=1 -> 1/7*(g=1?0:1):(g'=1)&(fd'=2) + 1/7*(g=2?0:1):(g'=2)&(fd'=2) + 1/7*(g=3?0:1):(g'=3)&(fd'=2) + 1/7*(g=4?0:1):(g'=4)&(fd'=2) + 1/7*(g=5?0:1):(g'=5)&(fd'=2) + 1/7*(g=6?0:1):(g'=6)&(fd'=2) + 1/7*(g=7?0:1):(g'=7)&(fd'=2) + 1/7*(g=8?0:1):(g'=8)&(fd'=2); // Deliver the mail, set current task to empty. [delivery] g=p & fd=2 -> 1 : (fd'=0); endmodule //------------------------------------------------------------------------------ label "outOfPower" = c=0;
This model is a DTMC like in the previous example. As the model includes several components, action labels (in square brackets) are used to implement synchronisations.
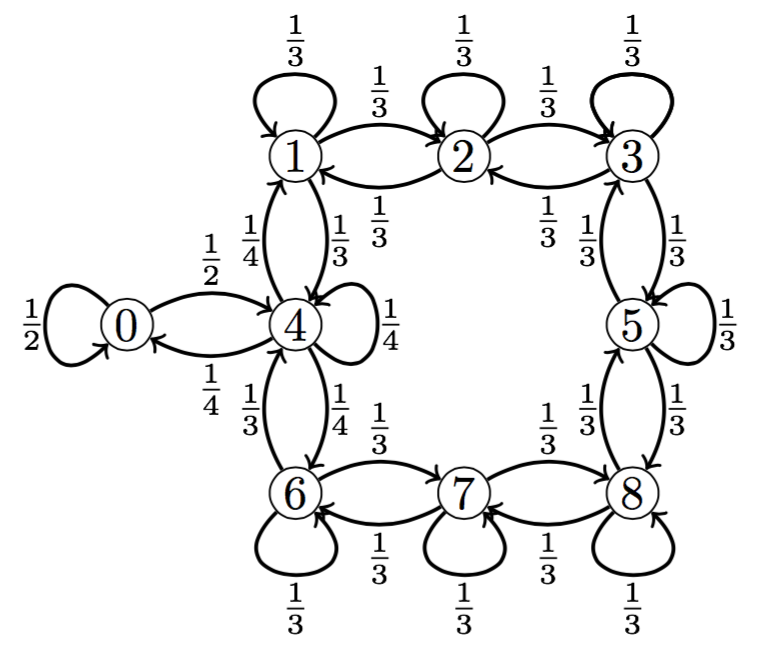
The controller module contains one variable representing the position (p) of the robot. It also reads the current status of the battery charge (c), but cannot update it as it belongs to another module. After a move, if its battery is not empty, the robot determines its next move by choosing uniformly a state among the available ones. If its battery is empty, then the robot is stuck. Assuming independence and when the battery is not empty, the controller module can be represented by the following DTMC.
The battery module records the charge of the battery in the variable c. It synchronises with the controller and updates the current charge of the battery according to the movement of the robot. When the robot position is 0, the battery recharges itself.
Read the
section
on synchronisation
in the manual.
Download
the model
file DeliveryRobot.pm
and load it into PRISM. Execute some paths through the model using
the simulator. You will see that there is also a label "outOfPower"
in the model, indicating that the battery is empty. For the moment
you can ignore the task module.
Compute
the probability to reach a state where the robot runs out of power.
Can you compute it by hand?
Write
down a CTL formula checking whether there exists a path that never
reaches a state where the robot is out of power.
Compute
the average number of moves that the robot can perform before
running out of power. To do so, add a reward structure that
synchronizes with transitions of the model as follows:
rewards "nbmove" [move] true : 1; endrewards
Such a reward was not necessary in the example of the die because, in the latter, we were counting the number of states in a trajectory, whereas here we are counting a specific kind of transitions.
You can
specify which reward structure to use in the property as follows:
R{"nbmove"}=? [F "outOfPower"]
The task module handles the next goal of the robot. The variable fd takes three values:
Compute
the average number of complete deliveries that the robot can perform
before running out of power. To do that, add a reward structure
synchronizing on [delivery].
Write down a CTL formula checking
whether there exists a path where the robot delivers an infinite number
of mails.
Leave the
value of the variable of batteryCharge
unspecified and make an experiment showing the influence of the
maximal battery charge on the average number of moves/deliveries.
Set the
value of batteryCharge back to 20.
Modify the probabilistic choice of the controller to increase the
mean number of moves and mean number of deliveries before running out
of power. Can you make these numbers arbitrarily high? Infinite?
A more systematic approach to build an efficient controller for the robot is to model the system as a Markov decision process (MDP). In an MDP, some choices of transitions are left unspecified. In the code below, all the probabilities of transitions of the controller are left unspecified.
mdp const int batteryCharge = 20; const int chargeSpeed = 4; const double f = 0.5; module controller p: [0..8] init 0; [move] p=0&c>0 -> (p'=0); [move] p=0&c>0 -> (p'=4); [move] p=4&c>0 -> (p'=0); [move] p=4&c>0 -> (p'=1); [move] p=4&c>0 -> (p'=4); [move] p=4&c>0 -> (p'=6); [move] p=1&c>0 -> (p'=4); [move] p=1&c>0 -> (p'=1); [move] p=1&c>0 -> (p'=2); [move] p=2&c>0 -> (p'=1); [move] p=2&c>0 -> (p'=2); [move] p=2&c>0 -> (p'=3); [move] p=3&c>0 -> (p'=2); [move] p=3&c>0 -> (p'=3); [move] p=3&c>0 -> (p'=5); [move] p=5&c>0 -> (p'=3); [move] p=5&c>0 -> (p'=5); [move] p=5&c>0 -> (p'=8); [move] p=6&c>0 -> (p'=4); [move] p=6&c>0 -> (p'=6); [move] p=6&c>0 -> (p'=7); [move] p=7&c>0 -> (p'=6); [move] p=7&c>0 -> (p'=7); [move] p=7&c>0 -> (p'=8); [move] p=8&c>0 -> (p'=5); [move] p=8&c>0 -> (p'=7); [move] p=8&c>0 -> (p'=8); [] c=0 -> 1.0 : true; endmodule module battery c: [0..batteryCharge] init batteryCharge; [move] c<=batteryCharge-chargeSpeed & p=0 -> 1.0 : (c'=c+chargeSpeed); [move] c>batteryCharge-chargeSpeed & p=0 -> 1.0 : (c'=batteryCharge); [move] c>0 & p!=0 -> 1.0 : (c'=c-1); endmodule module task g: [0..8] init 0; fd: [0..1] init 0; [move] g=0 -> f/8 : (g'=1) + f/8 : (g'=2) + f/8 : (g'=3) +f/8 : (g'=4) + f/8 : (g'=5) + f/8 : (g'=6) +f/8 : (g'=7) + f/8 : (g'=8) + 1-f: true ; [move] g!=0 & g!=p -> 1.0 : true; [] g!=0 & g=p & fd=0 -> 1/7*(g=1?0:1) : (g'=1)&(fd'=1) + 1/7*(g=2?0:1) : (g'=2)&(fd'=1) +1/7*(g=3?0:1) : (g'=3)&(fd'=1) + 1/7*(g=4?0:1) : (g'=4)&(fd'=1) +1/7*(g=5?0:1) : (g'=5)&(fd'=1) + 1/7*(g=6?0:1) : (g'=6)&(fd'=1) +1/7*(g=7?0:1) : (g'=7)&(fd'=1) + 1/7*(g=8?0:1) : (g'=8)&(fd'=1); [delivery] g!=0 & g=p & fd=1 -> 1 : (g'=0)&(fd'=0); endmodule label "outOfPower" = c=0; rewards "nbmove" [move] true :1.0 ; endrewards rewards "nbdelivery" [delivery] true :1.0 ; endrewards
Download
the file robotMDP and
load it into PRISM. Identify differences with the previous model.
The two things that changed compared to the previous model are the mdp keyword and the kind of model used for the controller module. Probabilities have been removed in the transitions and guards of transitions overlap.
Compute the probability to reach a state where the robot is out of power using
a controller that minimizes this probability, which can be done with the following property:
Pmin=? [F "outOfPower"]
You should get zero probability, meaning that there exists a controller such that the robot never runs out of power. Can you describe this controller? You can check that the number of moves and the number of deliveries before running out of power is infinite.
You can find out more about exporting optimal controllers by reading the adversaries section of the manual. Unfortunately, it is not yet possible to import the strategy into the simulator of PRISM using the graphical interface, but the PRISM-games extension supports this functionality.
Add a
constant T denoting time without specifying its initial value
in the model and perform experiments measuring the number of
expected deliveries depending on T.
You can use the following property:
R{"nbdelivery"}max=? [C<=T] / T
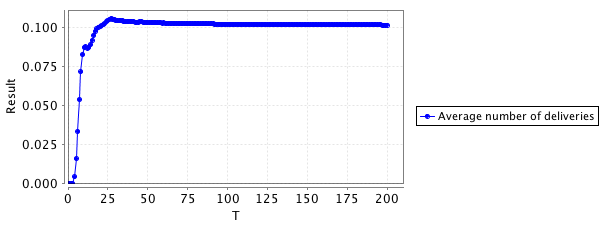
You should observe that, after a short transient period, the expected number of deliveries increases linearly with the time.
In the following, we set T to be equal to 200.
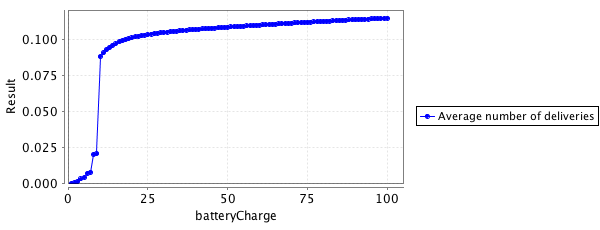
Perform experiments measuring the number of
expected deliveries, depending of
the value of the variable batteryCharge.
Next: Part C