[contributed by Maurice ter Beek, Mieke Massink, Diego Latella, Stefania Gnesi, Alessandro Forghieri and Maurizio Sebastianis]
Related publications: [BML+04, BML+05, BML05a, BML05b]
This case study is about using stochastic model checking to address a number of usability concerns that involve quantitative aspects of a user interface for the industrial groupware system thinkteam. thinkteam is a ready-to-use Product Data Management (PDM) application that was developed by think3 and which caters the product/document management needs of design processes in the manufacturing industry. It allows enterprises to capture, organise, automate, and share engineering product information in an efficient way and it is an example of an asynchronous and dispersed groupware system.
Many interesting properties of groupware protocols and their interfaces can be analysed a priori, i.e. before implementation, by means of a model-based approach and model-checking techniques. In fact, several aspects of the functional correctness, such as concurrency aspects and awareness aspects, of the groupware protocol underlying thinkteam (and of its planned publish/subscribe notification service) have indeed been addressed in several papers by means of a traditional model-checking approach. There are, however, also usability issues that are influenced by the performance of the groupware system rather than by its functional behaviour. One such issue was raised by the analysis of thinkteam with a traditional model-checking approach in [BML+04, BML+05]. It was shown that it was possible for the system to exclude a user from obtaining a file simply because other users competing for the same file were more "lucky" in their attempts to obtain the file. Such behaviour was explained by the fact that users were only provided with a file-access mechanism based on a retrial principle. While analysis with traditional model checking can be used to show that such a problem exists, it cannot be used to quantify the effect that it has on the user. In other words, it cannot be used to find out how often, in the average, a user needs to perform a retry in order to get a single file. Of course, the number of retries a user has to perform before obtaining a file is an important ingredient for measuring the usability of the system. If a high number of retries is necessary it may be more useful to have, e.g., a waiting list for files to which users can subscribe.
In this case study (taken from [BML05a, BML05b]) we investigate the trade-off between two different design options for granting users access to files in the database: a retrial approach and a waiting-list approach. As such, we show how stochastic model checking can be used for such analyses.
We now give a brief overview of thinkteam. For more information we refer to [BML+04] and www.think3.com.
thinkteam is a three-tier data management system running on Wintel platforms (cf. Figure 1). The most typical installation scenario is a network of desktop clients interacting with one centralized RDBMS server and one or more file servers. Components residing on each client node supply a graphical interface, metadata management, and integration services. Persistence services are achieved by building on the characteristics of the RDBMS and file servers. We describe only its vaulting subsystem, as it is relevant to our analysis.
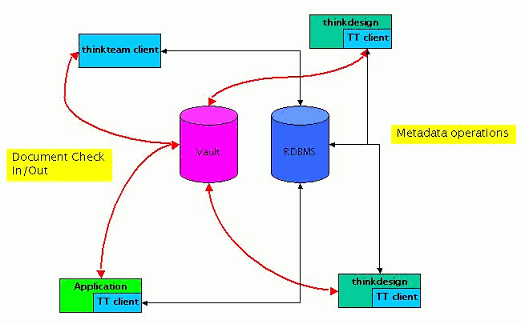
Controlled storage and retrieval of documents in PDM applications is traditionally called vaulting, the vault being a file-system-like repository. The two main functions of vaulting are: (1) to provide a single, secure, and controlled storage environment, where the documents controlled by the PDM application are managed, and (2) to prevent inconsistent updates or changes to the document base, while still allowing the maximal access compatible with the business rules. While the first function is subject to the implementation of the lower layers of the vaulting system, the second is implemented in thinkteam's underlying groupware protocol by a standard set of operations, viz.
It is important to note that access to documents (via the checkOut operation) is based on the "retrial" principle: currently there is no queue (or reservation system) handling the requests for editing rights on a document.
thinkteam typically handles some 100,000 documents for 20-100 users. A user rarely checks out more than 10 documents a day, but she can keep a document checked out from anywhere between 5 minutes and several days.
In order to maximize concurrency, a checkOut in thinkteam creates an exclusive lock for write access but not for read access. It is thus possible for clients to gain read access to documents that are checked out by others. An automatic solution of the write access conflict is not easy, as it is critically related to the type, nature, and scope of the changes that will be performed on the document. Moreover, standard but harsh solutions - like maintaining a dependency relation between documents and use it to simply lock all documents depending on the document being checked out - are out of the question for think3, as they would cause these documents to be unavailable for too long periods of time. For thinkteam, the preferred solution is thus to leave it to the users to resolve such conflicts. A publish/subscribe notification service provides the means to supply the clients with adequate information by
In [BML+04], several correctness properties of thinkteam have been verified. These properties addressed issues like concurrency control, awareness, and denial of service. Most properties were found to hold, with the exception of one concurrency-control property and a denial-of-service property. The problem with the concurrency-control property arises when a user simply "forever" forgets to checkIn the file it has checked out, which means that the lock on this file is never released. In thinkteam, such a situation is resolved by the intervention of a system administrator.
The problem with the denial-of-service property, on the other hand, is that it may be the case that one of the users can never get its turn to, e.g., perform a checkOut, simply because the system is continuously kept busy by the other users, while this user did express its desire to perform a checkOut. Such behaviour forms an integral part of the thinkteam protocol. This is because, as mentioned before, access to documents is based on the "retrial" principle: thinkteam currently has no queue (or reservation system) handling simultaneous requests for a document. Before simply extending thinkteam with a reservation system, it would be useful to know (1) how often, in the average, users have to express their requests before they are satisfied and (2) under which system conditions (number of users, file processing time, etc.) such a reservation system would really improve usability.
Next we describe the stochastic model of thinkteam in PEPA, first for the retrial approach and consequently for the waiting-list approach, and we perform several analyses on these models.
In Figure 2 the models of the User and CheckOut components, for the retrial approach, are drawn as automata for reasons of readability.
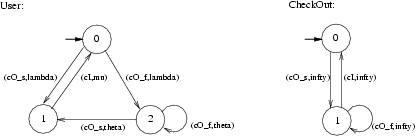
We consider the case that there is only one file, the (exclusive) access to which is handled by the CheckOut component. A user can express interest in checking out the file by performing a checkOut. This operation can either result in the user being granted the access to the file or in the user being denied the access because the file is currently already checked out by another user. In Figure 2, the successful execution of a checkOut is modelled by activity (cO_s,lambda), while a failed checkOut is modelled by (cO_f,lambda). The exponential rate lambda is also called the request rate. If the user does not obtain the file, then she may retry to check out the file, which is modelled by activity (cO_s,theta) in case of a successful retry and by (cO_f,theta) in case the checkOut failed. The exponential rate theta is also called the retrial rate. The checkIn operation, finally, is modelled by activity (cI,mu) and the exponential rate mu is also called the file processing rate. The CheckOut component takes care that only one user at a time can have the file in her possession. To this aim, it simply keeps track of whether the file is checked out (state <1>) or not (state <0>). When a User tries to obtain the file through the checkOut activity, then she is denied the file if it is currently checked out by another user while she might obtain the file if it is available.
The formal PEPA specifications of the User and the CheckOut component, and the composed model for three User components and the CheckOut component, are as follows:
lambda = 1.0; % request rate (user/hour) mu = 5.0; % file processing rate (user/hour) theta = 5.0; % retrial rate (user/hour) #User = (cO_s,lambda).User1 + (cO_f,lambda).User2; % request mode #User1 = (cI,mu).User; % file in possession #User2 = (cO_s,theta).User1 + (cO_f,theta).User2; % retry mode #CheckOut = (cO_s,infty).CheckOut1; #CheckOut1 = (cI,infty).CheckOut + (cO_f,infty).CheckOut1; (User <> User <> User) < cO_s,cO_f,cI > CheckOut |
We loaded these specifications into PRISM, which resulted in the following specification:
ctmc const double lambda = 1.0; const double mu = 5.0; const double theta = 5.0; const int User = 0; const int User1 = 1; const int User2 = 2; const int CheckOut = 0; const int CheckOut1 = 1; module User User_STATE : [0..2] init User; [cO_s] (User_STATE=User) -> lambda : (User_STATE'=User1); [cO_f] (User_STATE=User) -> lambda : (User_STATE'=User2); [cI] (User_STATE=User1) -> mu : (User_STATE'=User); [cO_s] (User_STATE=User2) -> theta : (User_STATE'=User1); [cO_f] (User_STATE=User2) -> theta : (User_STATE'=User2); endmodule module User_2 User_2_STATE : [0..2] init User; [cO_s] (User_2_STATE=User) -> lambda : (User_2_STATE'=User1); [cO_f] (User_2_STATE=User) -> lambda : (User_2_STATE'=User2); [cI] (User_2_STATE=User1) -> mu : (User_2_STATE'=User); [cO_s] (User_2_STATE=User2) -> theta : (User_2_STATE'=User1); [cO_f] (User_2_STATE=User2) -> theta : (User_2_STATE'=User2); endmodule module User_3 User_3_STATE : [0..2] init User; [cO_s] (User_3_STATE=User) -> lambda : (User_3_STATE'=User1); [cO_f] (User_3_STATE=User) -> lambda : (User_3_STATE'=User2); [cI] (User_3_STATE=User1) -> mu : (User_3_STATE'=User); [cO_s] (User_3_STATE=User2) -> theta : (User_3_STATE'=User1); [cO_f] (User_3_STATE=User2) -> theta : (User_3_STATE'=User2); endmodule module CheckOut CheckOut_STATE : [0..1] init CheckOut; [cO_s] (CheckOut_STATE=CheckOut) -> 1 : (CheckOut_STATE'=CheckOut1); [cI] (CheckOut_STATE=CheckOut1) -> 1 : (CheckOut_STATE'=CheckOut); [cO_f] (CheckOut_STATE=CheckOut1) -> 1 : (CheckOut_STATE'=CheckOut1); endmodule system ((User ||| (User_2 ||| User_3)) |[cO_s,cO_f,cI]| CheckOut) endsystem
From this specification PRISM generated a CTMC with 19 states and 54 transitions. Each state is represented as a quadruple (a,b,c,d), where a, b and c give the state in the User automaton of the first, the second and the third user, respectively, while d gives the state of automaton CheckOut. In Figure 3 we have drawn this CTMC and we have sketched how this CTMC is lumping equivalent to the much simpler CTMC given in Figure 4. (Moreover, the CTMC obtained by removing the self-loops from that of Figure 4 is frequently used in the theory of retrial queues [Fal90, FT97, Kul95].)
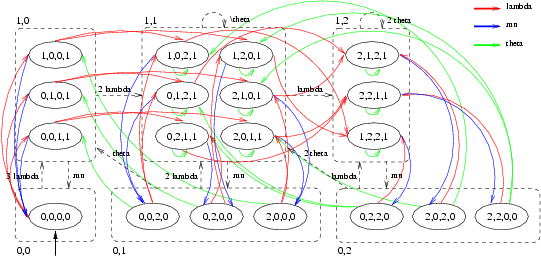
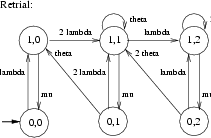
The states of this latter CTMC are tuples <x,y> in which x denotes whether the file is checked out (x = 1) or not (x = 0) and y = 0,1,2 denotes the number of users that are currently retrying to perform a checkOut. Note, however, that when a user inserts the file she has checked out back into the Vault through a checkIn activity, the CheckOut component does allow another user to checkOut the file but this need not be a user that has tried before to obtain the file. In fact, a race condition occurs between the request and retrial rates associated to the checkOut activity (cf.states <0,1> and <0,2>). Note also that once the file is checked in, it is not immediately granted to another user, even if there are users that have expressed their interest in obtaining the file. In such a situation, the file will remain unused for a period of time which is exponentially distributed with rate theta + lambda.
We will use the stochastic model and the stochastic logic to formalise and analyse various usability issues concerning the retrial approach used in thinkteam. In this context it is important to fix the time units one considers. We choose hours as our time unit. For instance, if mu = 5 this means that a typical user keeps the file in its possession for 60/5 = 12 minutes on the average.
While the above specifications assume three User components and one CheckOut component, our analyses below sometimes consider upto ten User components composed with one CheckOut component. Note that this leads to models that can no longer be verified by hand. For instance, the resulting composition in case of ten User components has a total of 6,143 states and 43,500 transitions and the lumping-equivalent CTMC has 20 states and 52 transitions.
All analyses reported below have been performed by running PRISM Version 2.0 and each took only a few seconds of CPU time. The iterative numerical method used for the computation of probabilities was Gauss-Seidel and the accuracy 1e-6.
We first analyse the probability that a user that has requested the file and is now in "retry mode" (state <2> of the User component), obtains the requested file within the next five hours. This measure can be formalised in CSL as (in a pseudo-notation close to the PRISM notation):
which must be read as follows: "what is the probability that path formula true U<=5 (User_STATE = 1) is satisfied for state User_STATE = 2?".
The results for this measure are presented in Figure 5 for request rate lambda = 1 (i.e. a user requests the file once an hour on average), retrial rate theta taking values 1, 5 and 10 (i.e. in one hour a user averagely retries one, five or ten times to obtain the file), file processing rate mu = 1 (i.e. a user in the average keeps the file checked out for one hour) and for different numbers of users ranging from 1 to 10.
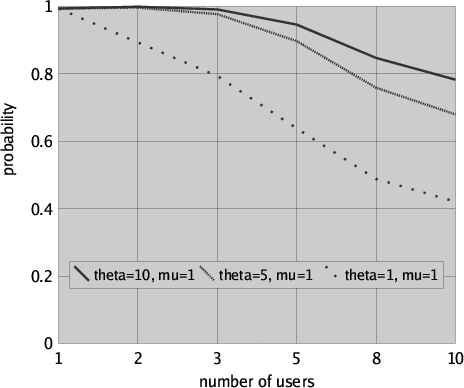
Clearly, with an increasing number of users the probability that a user gets her file within the time interval is decreasing. On the other hand, with an increasing retrial rate and an invaried file processing rate the probability for a user to obtain the requested file within the time interval is increasing. Further results could easily be obtained by model checking for different rate parameters that may characterise different profiles of use of the same system. In particular, this measure could be used to evaluate under which circumstances (e.g. when it is known that only a few users will compete for the same file) a retrial approach would give satisfactory results from a usability point of view.
A somewhat more complicated measure can be obtained with some additional calculations involving steady-state analysis (by means of model checking). Figure 6 shows the average number of retrials per file request for request rate lambda = 1, retrial rate theta taking values 5 and 10, file processing rate mu ranging from 1 to 10 and for 10 users. The measure has been computed as the average number of retries that take place over a certain system observation period of time T divided by the average number of requests during T. To compute the average number of retries (requests, resp.) we proceeded as follows. We first compute the steady-state probability p (q, resp.) of the user being in "retry mode" ("request mode", resp.), i.e.
The fraction of time the user is in "retry mode" ("request mode", resp.) is then given by T ⋅ p (T ⋅ q, resp.). Consequently the average number of retries (requests, resp.) is theta ⋅ T ⋅ p (lambda ⋅ T ⋅ q, resp.). Hence the measure of interest is (theta ⋅ p)/(lambda ⋅ q).
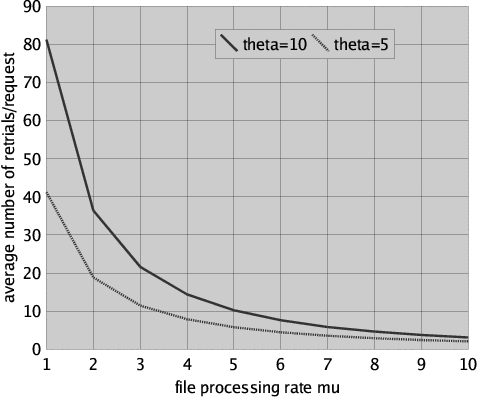
It is easy to observe in Figure 6 that the number of retrials decreases considerably when the file processing rate is increased (i.e. when the users restitute, by means of a checkIn, the file they had checked out after a shorter time). We also note that a relatively high file processing rate is needed for obtaining an acceptably low number of retrials in the case of 10 users that regularly compete for the same file.
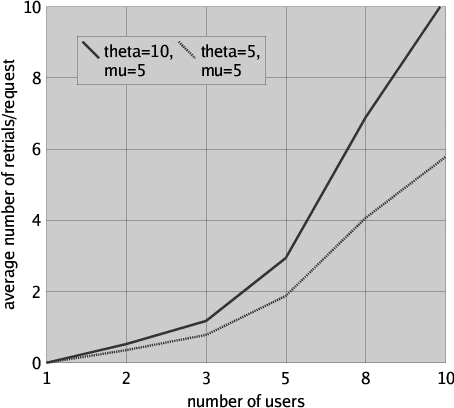
The effect on the average number of retries is even better illustrated in Figure 7, where with a similar approach as outlined above the average number of retrials per file request is presented for request rate lambda = 1, retrial rate theta taking values 5 and 10, fixed file processing rate mu = 5 and various numbers of users. Clearly, the average number of retrials per file request increases sharply when the number of users increases.
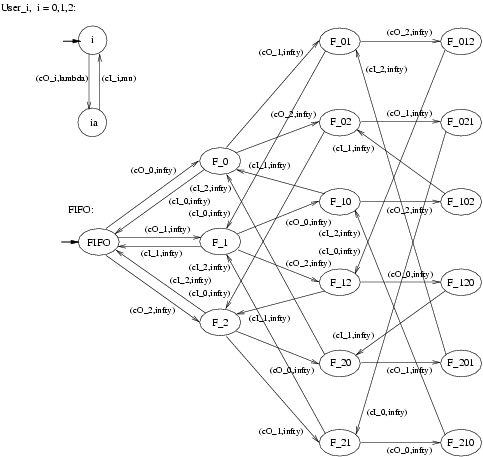
We again use PEPA to specify our model and we draw the models as automata for readability. In contrast with our model for the retrial approach, we now assume that a user that attempts to checkOut the file when it has already been checked out by another user is put in a FIFO queue. The moment in which the file then becomes available, the user that is first in this FIFO queue obtains the file. This implies the following changes w.r.t. the model from the previous section. Since a user no longer retries to obtain the file after her initial unsuccessful attempt to checkOut the file, the new User component has two states only, viz. state <2> is removed from the User component as given in Figure 2. Moreover, since the CheckOut component now implements a FIFO policy, the new CheckOut component needs to keep track of the number of users in the FIFO queue and their relative position. This also means that the new CheckOut component needs to know exactly which of the users performs a checkOut or a checkIn. In Figure 8 the model of the new Users and CheckOut - now called FIFO - components are drawn.
The formal PEPA specifications of these new Users and CheckOut components, and the composed model for three User components and the CheckOut component, are as follows:
lambda = 1.0; % request rate mu = 5.0; % file processing rate #User_0 = (cO_0,lambda).User_0a; #User_0a = (cI_0,mu).User_0; #User_1 = (cO_1,lambda).User_1a; #User_1a = (cI_1,mu).User_1; #User_2 = (cO_2,lambda).User_2a; #User_2a = (cI_2,mu).User_2; #FIFO = (cO_0,infty).F_0 + (cO_1,infty).F_1 + (cO_2,infty).F_2; #F_0 = (cI_0,infty).FIFO + (cO_1,infty).F_01 + (cO_2,infty).F_02; #F_1 = (cI_1,infty).FIFO + (cO_0,infty).F_10 + (cO_2,infty).F_12; #F_2 = (cI_2,infty).FIFO + (cO_0,infty).F_20 + (cO_1,infty).F_21; #F_01 = (cI_0,infty).F_1 + (cO_2,infty).F_012; #F_02 = (cI_0,infty).F_2 + (cO_1,infty).F_021; #F_10 = (cI_1,infty).F_0 + (cO_2,infty).F_102; #F_12 = (cI_1,infty).F_2 + (cO_0,infty).F_120; #F_20 = (cI_2,infty).F_0 + (cO_1,infty).F_201; #F_21 = (cI_2,infty).F_1 + (cO_0,infty).F_210; #F_012 = (cI_0,infty).F_12; #F_021 = (cI_0,infty).F_21; #F_102 = (cI_1,infty).F_02; #F_120 = (cI_1,infty).F_20; #F_201 = (cI_2,infty).F_01; #F_210 = (cI_2,infty).F_10; (User_0 <> User_1 <> User_2) < cO_0,cO_1,cO_2,cI_0,cI_1,cI_2 > FIFO |
The translations of these specifications into the PRISM language are as follows:
ctmc const double lambda = 1.0; const double mu = 5.0; const int User_0 = 0; const int User_0a = 1; const int User_1 = 0; const int User_1a = 1; const int User_2 = 0; const int User_2a = 1; const int FIFO_empty = 0; const int F_0 = 1; const int F_01 = 2; const int F_012 = 3; const int F_02 = 4; const int F_021 = 5; const int F_1 = 6; const int F_10 = 7; const int F_102 = 8; const int F_12 = 9; const int F_120 = 10; const int F_2 = 11; const int F_20 = 12; const int F_201 = 13; const int F_21 = 14; const int F_210 = 15; module User_0 User_0_STATE : [0..1] init User_0; [cO_0] (User_0_STATE=User_0) -> lambda : (User_0_STATE'=User_0a); [cI_0] (User_0_STATE=User_0a) -> mu : (User_0_STATE'=User_0); endmodule module User_1 User_1_STATE : [0..1] init User_1; [cO_1] (User_1_STATE=User_1) -> lambda : (User_1_STATE'=User_1a); [cI_1] (User_1_STATE=User_1a) -> mu : (User_1_STATE'=User_1); endmodule module User_2 User_2_STATE : [0..1] init User_2; [cO_2] (User_2_STATE=User_2) -> lambda : (User_2_STATE'=User_2a); [cI_2] (User_2_STATE=User_2a) -> mu : (User_2_STATE'=User_2); endmodule module FIFO_empty FIFO_empty_STATE : [0..15] init FIFO_empty; [cO_0] (FIFO_empty_STATE=FIFO_empty) -> 1 : (FIFO_empty_STATE'=F_0); [cO_1] (FIFO_empty_STATE=FIFO_empty) -> 1 : (FIFO_empty_STATE'=F_1); [cO_2] (FIFO_empty_STATE=FIFO_empty) -> 1 : (FIFO_empty_STATE'=F_2); [cI_0] (FIFO_empty_STATE=F_0) -> 1 : (FIFO_empty_STATE'=FIFO_empty); [cO_1] (FIFO_empty_STATE=F_0) -> 1 : (FIFO_empty_STATE'=F_01); [cO_2] (FIFO_empty_STATE=F_0) -> 1 : (FIFO_empty_STATE'=F_02); [cI_0] (FIFO_empty_STATE=F_01) -> 1 : (FIFO_empty_STATE'=F_1); [cO_2] (FIFO_empty_STATE=F_01) -> 1 : (FIFO_empty_STATE'=F_012); [cI_0] (FIFO_empty_STATE=F_012) -> 1 : (FIFO_empty_STATE'=F_12); [cI_0] (FIFO_empty_STATE=F_02) -> 1 : (FIFO_empty_STATE'=F_2); [cO_1] (FIFO_empty_STATE=F_02) -> 1 : (FIFO_empty_STATE'=F_021); [cI_0] (FIFO_empty_STATE=F_021) -> 1 : (FIFO_empty_STATE'=F_21); [cI_1] (FIFO_empty_STATE=F_1) -> 1 : (FIFO_empty_STATE'=FIFO_empty); [cO_0] (FIFO_empty_STATE=F_1) -> 1 : (FIFO_empty_STATE'=F_10); [cO_2] (FIFO_empty_STATE=F_1) -> 1 : (FIFO_empty_STATE'=F_12); [cI_1] (FIFO_empty_STATE=F_10) -> 1 : (FIFO_empty_STATE'=F_0); [cO_2] (FIFO_empty_STATE=F_10) -> 1 : (FIFO_empty_STATE'=F_102); [cI_1] (FIFO_empty_STATE=F_102) -> 1 : (FIFO_empty_STATE'=F_02); [cI_1] (FIFO_empty_STATE=F_12) -> 1 : (FIFO_empty_STATE'=F_2); [cO_0] (FIFO_empty_STATE=F_12) -> 1 : (FIFO_empty_STATE'=F_120); [cI_1] (FIFO_empty_STATE=F_120) -> 1 : (FIFO_empty_STATE'=F_20); [cI_2] (FIFO_empty_STATE=F_2) -> 1 : (FIFO_empty_STATE'=FIFO_empty); [cO_0] (FIFO_empty_STATE=F_2) -> 1 : (FIFO_empty_STATE'=F_20); [cO_1] (FIFO_empty_STATE=F_2) -> 1 : (FIFO_empty_STATE'=F_21); [cI_2] (FIFO_empty_STATE=F_20) -> 1 : (FIFO_empty_STATE'=F_0); [cO_1] (FIFO_empty_STATE=F_20) -> 1 : (FIFO_empty_STATE'=F_201); [cI_2] (FIFO_empty_STATE=F_201) -> 1 : (FIFO_empty_STATE'=F_01); [cI_2] (FIFO_empty_STATE=F_21) -> 1 : (FIFO_empty_STATE'=F_1); [cO_0] (FIFO_empty_STATE=F_21) -> 1 : (FIFO_empty_STATE'=F_210); [cI_2] (FIFO_empty_STATE=F_210) -> 1 : (FIFO_empty_STATE'=F_10); endmodule system ((User_0 ||| (User_1 ||| User_2)) |[cO_0,cO_1,cO_2,cI_0,cI_1,cI_2]| FIFO_empty) endsystem
From these specifications PRISM automatically generates a CTMC with 16 states and 30 transitions. In Figure 9 we have drawn this CTMC and we have sketched how this CTMC is lumping equivalent to the much simpler CTMC given in Figure 10.
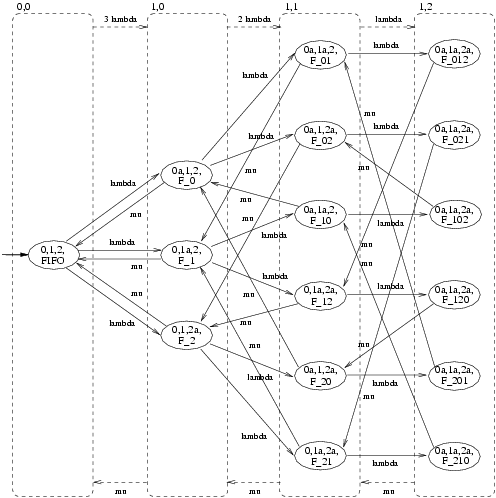
It is not difficult to verify that the CTMC of Figure 9 is indeed lumping equivalent to the CTMC of Figure 10.

The state tuples of this CTMC have the same meaning as before, but states <0,1> and <0,2> no longer occur. This is due to the fact that, once the file is checked in, it is immediately granted to another user, viz. the first in the FIFO queue.
The fact that we consider an exponential request rate lambda, an exponential file processing rate mu, one file, and three users means that we are dealing with a M|M|1|3 queueing system [Hav01, Kul95]. The CTMC of Figure 10 is then its underlying CTMC and this type of CTMC is also called a birth-death process [Hav01, Kul95].
We now compare the two models with respect to the steady-state probability that there are users waiting to obtain the file after a checkOut request. To measure this we compute the probabilities for at least one user not being granted the file after asking for it, i.e. the steady-state probability p to be in a state in which at least one user has performed a checkOut but did not obtain the file yet. In the retrial approach this concerns the situation in which any of the User components of Figure 2 is in state <2>, whereas in the waiting-list approach this concerns the situation in which two or three of the new User components of Figure 8 are in state <ia>, i = 0,1,2. Hence this can be expressed as CSL steady-state formulae (again in a pseudo-notation close to that of PRISM):
in the retrial approach while
in the waiting-list approach.
The results of our comparison are presented in Figure 11 for request rate lambda = 1, retrial rate theta (only in the retrial approach of course) ranging from 1 to 10, file processing rate mu taking values 5 and 10 and 3 users.
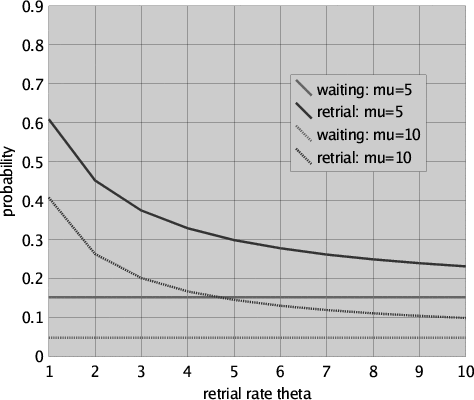
It is easy to see that, as expected, the waiting-list approach outperforms the retrial approach in all the cases we considered: The probability to be in a situation in which two or three of the new User components of the waiting-list approach are in state <ia>, i = 0,1,2, is always lower than the probability to be in a situation in which any of the User components of the retrial approach is in state <2>. Note that for large theta the probability in case of the retrial approach is asymptotically approaching that of the waiting-list approach, of course given the same values for lambda and mu. While we did verify this for values of theta upto 109, it is of course extremely unrealistic to assume that a user performs 109 retries per hour. We thus conclude that the time that a user has to wait "in the long run" for the file after it has performed a checkOut is always less in the waiting-list approach than in the retrial approach. Furthermore, while increasing the retrial rate (i.e. reducing the time inbetween retries) does bring the results for the retrial approach close to those for the waiting-list approach, it takes highly unrealistic retrial rates to reach a difference between the two approaches that is insignificantly small.
Above we have addressed the formal analysis of a number of quantitative usability measures of a small, but relevant industrial case study concerning an existing groupware system for PDM, thinkteam. We have shown how the quantitative aspects of the interaction between users and the system can be modelled in PEPA. The model has been used to obtain quantitative information on two different approaches for users to obtain files from a central database; one based on retrial and one based on a reservation system implemented via a FIFO waiting list. The quantitative measures addressed the expected time that users are required to wait before they obtain a requested file and the average number of retries per file, for various assumptions on the parameters of the model. These measures have been formalised as formulae of CSL and analysed by means of PRISM.
The results show that, from a user perspective, the retrial approach is less convenient than the waiting-list approach. Moreover, it can be shown that the situation for the retrial approach rapidly deteriorates with an increasing number of users that compete for the same file. Nevertheless, in situations where it is very unlikely that more than a few users compete for the same file the retrial approach may still be acceptable from a usability point of view, even if not optimal. The use of stochastic model checking allowed for a convenient modular and compositional specification of the system and the automatic generation of the underlying CTMCs on which performance analysis is based. Furthermore, the combination of compositional specification of models and logic characterisation of measures of interest provides a promising technique for a priori formal model-based usability analysis where quantitative aspects as well as qualitative ones are involved.
We plan to apply the developed models and measures for the analysis of different user profiles of the actual thinkteam system in collaboration with think3. The user profiles will be useful to obtain realistic values for the parameters of the model and for further validation of the model. In a further extension of the model we also plan to deal with the quantitative effects of the addition of a publish/subscribe notification service to thinkteam.
Feel free to contact us if you have any questions about the case study presented here.