(Huang and Ferrell)
Related publications: [KNP08a]
The MAP (Mitogen-Activated Protien) Kinases are involved in a pathway through which information is sent to the nucleus. It is one of the most important signalling pathways since it plays a pivotal role in the molecular-signalling that governs the growth, proliferation and survival of many cell types. The MAPK cascade consists of a MAPK Kinase Kinase (MAPKKK), MAPK Kinase (MAPKK) and a MAPK. The cascade is initialised through the phosphorylation of MAPKKK, which then activates MAPKK through the phosphorylation at two serine residues and this then activates MAPK through the phosphorylation at theronine and tyrosine residues. The initialisation can be caused by a diverse set of stimuli including growth factors, neurotransmitters and cytokines.
The model of the pathway we consider is taken from [HF96]. Its structure is given below.
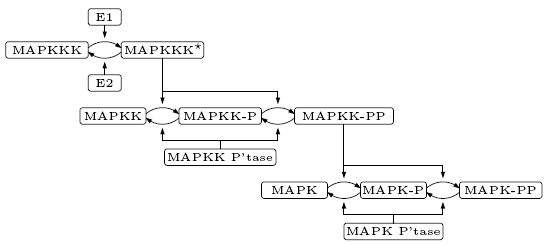
Following [HF96], we assume that the phosphorylation of both MAPK and MAPKK occur in two distributed steps. For example, when MAPK collides with its activator (MAPKK-PP) the first phosphorylation (MAPK-P) occurs and the activator is released. The phosphorylated MAPK must then collide again with its activator for the second phosphorylation (MAPK-PP) to occur. The deactivation of phosphorylated MAPK and MAPKK is caused by the corresponding phosphatase, while the activation and deactivation of MAPKKK is through the enzymes E1 and E2 respectively. To simplify the presentation we denote MAPK, MAPKK and MAPKKK by K, KK and KKK respectively.
| 1. MAPKKK is activated through enzyme E1 | ||
| KKK + E1 → KKK:E1 (a1 = 1 nM-1s-1) KKK + E1 ← KKK:E1 (d1 = 150 s-1) KKK:E1 → KKK* + E1 (k1 = 150 s-1) | ||
| 2. MAPKKK is deactivated through enzyme E2 | ||
| KKK* + E2 → KKK:E2 (a2 = 1 nM-1s-1) KKK* + E2 ← KKK:E2 (d2 = 150 s-1) KKK*:E2 → KKK + E2 (k2 = 150 s-1) | ||
| 3. MAPKK is activated by MAPKKK* | ||
| KK + KKK* → KK:KKK* (a3 = 1 nM-1s-1) KK + KKK* ← KK:KKK* (d3 = 150 s-1) KK:KKK* → KK-P + KKK* (k3 = 150 s-1) | ||
| 4. MAPKK-P is deactivated by MAPKK phosphatase | ||
| KK-P + KK-Ptase → KK-P:KK-Ptase (a4 = 1 nM-1s-1) KK-P + KK-Ptase ← KK-P:KK-Ptase (d4 = 150 s-1) KK-P:KK-Ptase → KK + KK-Ptase (k4 = 150 s-1) | ||
| 5. MAPKK-P is activated by MAPKKK* | ||
| KK-P + KKK* → KK-P:KKK* (a5 = 1 nM-1s-1) KK-P + KKK* ← KK-P:KKK* (d5 = 150 s-1) KK-P:KKK* → KK-PP + KKK* (k5 = 150 s-1) | ||
| 6. MAPKK-PP is deactivated by MAPKK phosphatase | ||
| KK-PP + KK-Ptase → KK-PP:KK-Ptase (a6 = 1 nM-1s-1) KK-PP + KK-Ptase ← KK-PP:KK-Ptase (d6 = 150 s-1) KK-PP:KK-Ptase → KK-P + KK-Ptase (k6 = 150 s-1) | ||
| 7. MAPK is activated by MAPKK-PP | ||
| K + KK-PP → K:KK-PP (a7 = 1 nM-1s-1) K + KK-PP ← K:KK-PP (d7 = 150 s-1) K:KK-PP → K-P + KK-PP (k7 = 150 s-1) | ||
| 8. MAPK-P is deactivated by MAPK phosphatase | ||
| K-P + K-Ptase → K-P:K-Ptase (a8 = 1 nM-1s-1) K-P + K-Ptase ← K-P:K-Ptase (d8 = 150 s-1) K-P:K-Ptase → K + K-Ptase (k8 = 150 s-1) | ||
| 9. MAPK-P is activated by MAPKK-PP | ||
| K-P + KK-PP → K-P:KK-PP (a9 = 1 nM-1s-1) K-P + KK-PP ← K-P:KK-PP (d9 = 150 s-1) K-P:KK-PP → K-PP + KK-PP (k9 = 150 s-1) | ||
| 10. MAPK-PP is deactivated by MAPK phosphatase | ||
| K-PP + K-Ptase → K-PP:K-Ptase (a10 = 1 nM-1s-1) K-PP + K-Ptase ← K-PP:K-Ptase (d10 = 150 s-1) K-PP:K-Ptase → K-P + K-Ptase (k10 = 150 s-1) | ||
The kinetic rates are based on the data presented in [HF96] where it is assumed the Km values (Km = (dm + km) / am) for the phosphorylation and dephosphorylation of MAPK, MAPKK and MAPKK all equal 300 nM.
When building a PRISM model of a biological pathway, it is possible to construct an individual-based model which provides a detailed model of the evolution of individual molecular components. However, taking this approach comes at a cost: it will inevitably suffer from the well known state-space explosion problem where, as the complexity of the system increases, the state space of the underlying model grows exponentially.
An alternative is to employ a population-based approach where the number of each type of molecule or species is modelled, rather than the state of each individual component. Such an approach leads to a much smaller state-space (see for example [HKN+08]) while still including sufficient detail to express the properties of interest. For these reasons, it is this approach that we use here.
We now describe the specification in PRISM of the MAPK cascade from the previous section. Each of the basic elements of the pathway (MAPKKK, MAPKK, MAPK, MAPKK Phosphatase, MAPK Phosphatase, E1 and E2), is represented by a separate PRISM module and synchronisation between modules is used to model reactions which involve interactions between multiple elements. However, the different forms which each can take (for example, which other compounds it is bound to) are represented by one or more variables within the module.
The PRISM model for the pathway is given below.
// MAPK cascade // taken from: C.-Y. Huang and J. Ferrell // Ultrasensitivity in the mitgen-activated protein kinase cascade // Proc. Natl. Acad. Sci. 93:10078-13100, 1996 // gxn/dxp 19/12/07 ctmc // constants (number of elements of each species) const int E1=1; // initial amount of E1 const int E2=1; // initial amount of E2 const int M=1; // initial amount of MAPK phosphatase and MAPKK phosphatase const int N; // initial amount of MAPK/MAPKK and MAPKKK // reaction rates (suppose volume proportional to the number of elements of MAPK) const double a1=1/N; const double d1=150; const double k1=150; const double a2=1/N; const double d2=150; const double k2=150; const double a3=1/N; const double d3=150; const double k3=150; const double a4=1/N; const double d4=150; const double k4=150; const double a5=1/N; const double d5=150; const double k5=150; const double a6=1/N; const double d6=150; const double k6=150; const double a7=1/N; const double d7=150; const double k7=150; const double a8=1/N; const double d8=150; const double k8=150; const double a9=1/N; const double d9=150; const double k9=150; const double a10=1/N; const double d10=150; const double k10=150; //------------------------------------------------------------------------------ // enzymes module E1 e1 : [0..E1] init E1; // amount of enzyme E1 // reaction 1 (MAPKKK is activated by E1) [a_kkk_e1] e1>0 -> e1 : (e1'=e1-1); [d_kkk_e1] e1<E1 -> 1 : (e1'=e1+1); [k_kkk_e1] e1<E1 -> 1 : (e1'=e1+1); endmodule // construct E2 by renaming E1 module E2 = E1[ e1=e2, E1=E2, a_kkk_e1=a_kkk_e2, d_kkk_e1=d_kkk_e2, k_kkk_e1=k_kkk_e2 ] endmodule //------------------------------------------------------------------------------ // phosphatases // mapk phosphatases module KPTASE kptase : [0..M] init M; // amount of MAPK Phosphatase // reactions 8 and 10 (MAPK/MAPK-P is deactivated by MAPK Phosphatase) [a_k_ptase] kptase>0 -> kptase : (kptase'=kptase-1); [d_k_ptase] kptase<M -> 1 : (kptase'=kptase+1); [k_k_ptase] kptase<M -> 1 : (kptase'=kptase+1); endmodule // construct mapkk phosphatases by renaming module for mapk phosphatases module KKPTASE = KPTASE[ kptase= kkptase, a_k_ptase=a_kk_ptase, d_k_ptase=d_kk_ptase, k_k_ptase=k_kk_ptase ] endmodule //------------------------------------------------------------------------------ // mapks // mapk module MAPK k : [0..N] init N; // quantity of MAPK k_kkpp : [0..N] init 0; // quantity of MAPK:MAPKK-PP kp : [0..N] init 0; // quantity of MAPK-P kp_kkpp : [0..N] init 0; // quantity of MAPK-P:MAPKK-PP kp_ptase : [0..N] init 0; // quantity of MAPK-P:MAPK Phosphatase kpp : [0..N] init 0; // quantity of MAPK-PP kpp_ptase : [0..N] init 0; // quantity of MAPK-PP:MAPK Phosphatase // reaction 7 (MAPK is activated by MAPKK-PP) [a_k_kk] k>0 & k_kkpp<N -> a7*k : (k_kkpp'=k_kkpp+1) & (k'=k-1); [d_k_kk] k<N & k_kkpp>0 -> d7*k_kkpp : (k_kkpp'=k_kkpp-1) & (k'=k+1); [k_k_kk] k_kkpp>0 & kp<N -> k7*k_kkpp : (k_kkpp'=k_kkpp-1) & (kp'=kp+1); // reaction 8 (MAPK-P is deactivated by MAPK Phosphatase) [a_k_ptase] kp>0 & kp_ptase<N -> a8*kp : (kp_ptase'=kp_ptase+1) & (kp'=kp-1); [d_k_ptase] kp<N & kp_ptase>0 -> d8*kp_ptase : (kp_ptase'=kp_ptase-1) & (kp'=kp+1); [k_k_ptase] kp_ptase>0 & k<N -> k8*kp_ptase : (kp_ptase'=kp_ptase-1) & (k'=k+1); // reaction 9 (MAPK-P is activated by MAPKK-PP) [a_k_kk] kp>0 & kp_kkpp<N -> a9*kp : (kp_kkpp'=kp_kkpp+1) & (kp'=kp-1); [d_k_kk] kp<N & kp_kkpp>0 -> d9*kp_kkpp : (kp_kkpp'=kp_kkpp-1) & (kp'=kp+1); [k_k_kk] kp_kkpp>0 & kpp<N -> k9*kp_kkpp : (kp_kkpp'=kp_kkpp-1) & (kpp'=kpp+1); // reaction 10 (MAPK-P is deactivated by MAPK Phosphatase) [a_k_ptase] kpp>0 & kpp_ptase<N -> a10*kpp : (kpp_ptase'=kpp_ptase+1) & (kpp'=kpp-1); [d_k_ptase] kpp<N & kpp_ptase>0 -> d10*kpp_ptase : (kpp_ptase'=kpp_ptase-1) & (kpp'=kpp+1); [k_k_ptase] kpp_ptase>0 & kp<N -> k10*kpp_ptase : (kpp_ptase'=kpp_ptase-1) & (kp'=kp+1); endmodule // mapkk module MAPKK kk : [0..N] init N; // quantity of MAPKK kk_kkkp : [0..N] init 0; // quantity of MAPKK:MAPKKK-P kkp : [0..N] init 0; // quantity of MAPKK-P kkp_kkkp : [0..N] init 0; // quantity of MAPKK-P:MAPKKK-P kkp_ptase : [0..N] init 0; // quantity of MAPKK-P:MAPKK Phosphatase kkpp : [0..N] init 0; // quantity of MAPKK-PP kkpp_ptase : [0..N] init 0; // quantity of MAPKK-PP:MAPKK Phosphatase // reaction 3 (MAPKK is activated by MAPKKK*) [a_kk_kkk] kk>0 & kk_kkkp<N -> a3*kk : (kk_kkkp'=kk_kkkp+1) & (kk'=kk-1); [d_kk_kkk] kk<N & kk_kkkp>0 -> d3*kk_kkkp : (kk_kkkp'=kk_kkkp-1) & (kk'=kk+1); [k_kk_kkk] kk_kkkp>0 & kkp<N -> k3*kk_kkkp : (kk_kkkp'=kk_kkkp-1) & (kkp'=kkp+1); // reaction 4 (MAPKK-P is deactivated by MAPKK Phosphatase) [a_kk_ptase] kkp>0 & kkp_ptase<N -> a4*kkp : (kkp_ptase'=kkp_ptase+1) & (kkp'=kkp-1); [d_kk_ptase] kkp<N & kkp_ptase>0 -> d4*kkp_ptase : (kkp_ptase'=kkp_ptase-1) & (kkp'=kkp+1); [k_kk_ptase] kkp_ptase>0 & kk<N -> k4*kkp_ptase : (kkp_ptase'=kkp_ptase-1) & (kk'=kk+1); // reaction 5 (MAPKK-P is activated by MAPKKK*) [a_kk_kkk] kkp>0 & kkp_kkkp<N -> a5*kkp : (kkp_kkkp'=kkp_kkkp+1) & (kkp'=kkp-1); [d_kk_kkk] kkp<N & kkp_kkkp>0 -> d5*kkp_kkkp : (kkp_kkkp'=kkp_kkkp-1) & (kkp'=kkp+1); [k_kk_kkk] kkp_kkkp>0 & kkpp<N -> k5*kkp_kkkp : (kkp_kkkp'=kkp_kkkp-1) & (kkpp'=kkpp+1); // reaction 6 (MAPKK-P is deactivated by MAPKK Phosphatase) [a_kk_ptase] kkpp>0 & kkpp_ptase<N -> a6*kkpp : (kkpp_ptase'=kkpp_ptase+1) & (kkpp'=kkpp-1); [d_kk_ptase] kkpp<N & kkpp_ptase>0 -> d6*kkpp_ptase : (kkpp_ptase'=kkpp_ptase-1) & (kkpp'=kkpp+1); [k_kk_ptase] kkpp_ptase>0 & kkp<N -> k6*kkpp_ptase : (kkpp_ptase'=kkpp_ptase-1) & (kkp'=kkp+1); // reactions 7 and 9 (MAPK/MAPK-P is activated by MAPKPP) [a_k_kk] kkpp>0 -> kkpp : (kkpp'=kkpp-1); [d_k_kk] kkpp<N -> 1 : (kkpp'=kkpp+1); [k_k_kk] kkpp<N -> 1 : (kkpp'=kkpp+1); endmodule // mapkkk module MAPKKK kkk : [0..N] init N; // quantity of MAPKKK kkk_e1 : [0..N] init 0; // quantity of MAPKKK:E1 kkkp : [0..N] init 0; // quantity of MAPKKK* kkkp_e2 : [0..N] init 0; // quantity of MAPKKK*:E2 // reaction 1 (MAPKKK is activated by E1) [a_kkk_e1] kkk>0 & kkk_e1<N -> a1*kkk : (kkk_e1'=kkk_e1+1) & (kkk'=kkk-1); [d_kkk_e1] kkk<N & kkk_e1>0 -> d1*kkk_e1 : (kkk_e1'=kkk_e1-1) & (kkk'=kkk+1); [k_kkk_e1] kkk_e1>0 & kkkp<N -> k1*kkk_e1 : (kkk_e1'=kkk_e1-1) & (kkkp'=kkkp+1); // reaction 2 (MAPKKK* is deactivated by E2) [a_kkk_e2] kkkp>0 & kkkp_e2<N -> a2*kkkp : (kkkp_e2'=kkkp_e2+1) & (kkkp'=kkkp-1); [d_kkk_e2] kkkp<N & kkkp_e2>0 -> d2*kkkp_e2 : (kkkp_e2'=kkkp_e2-1) & (kkkp'=kkkp+1); [k_kkk_e2] kkkp_e2>0 & kkk<N -> k2*kkkp_e2 : (kkkp_e2'=kkkp_e2-1) & (kkk'=kkk+1); // reactions 3 and 5 (MAPKK/MAPKK-P is activated by MAPKKP) [a_kk_kkk] kkkp>0 -> kkkp : (kkkp'=kkkp-1); [d_kk_kkk] kkkp<N -> 1 : (kkkp'=kkkp+1); [k_kk_kkk] kkkp<N -> 1 : (kkkp'=kkkp+1); endmodule //------------------------------------------------------------------------------ // reward structures rewards "activated" // activated mapk true : kpp; endrewards rewards "activated_squared" // activated mapk squared (used to calculate standard deviation) true : kpp*kpp; endrewards rewards "percentage" //percentage activated mapk true : 100*(kpp/N); endrewards rewards "reactions" // reactions between mapk and mapkk [a_k_kk] true : 1; [d_k_kk] true : 1; [k_k_kk] true : 1; endrewards rewards "time" // time true : 1; endrewards
We have included five reward structures in the description. The first reward structure (''activated'') assigns a state reward equal to the amount of MAPK that is activated while the second reward structure (''activated_squared'') assigns a state reward equal to the square of the amount MAPK that is activated. Since, the standard deviation of a random variable X equals the square root of its variance which equals:
together these rewards can be used to compute the standard deviation (and variance) of random variable for the amount of activated MAPK at a time instant. The third (''activated'') assigns a state reward equal to the percentage of MAPK that is activated. The forth reward structure (''reactions'') assigns a reward of 1 to all transitions which correspond to a reaction between MAPK and MAPKK and the last (''time'') simply assigns a state reward of 1 to all states in the model.
The table below shows statistics for the MTBDD which represents each model we have built, in terms of the number of states, transitions, the total number of nodes and the number of leaves (terminal nodes).
| N | States | Transitions | Nodes | Leaves | |
| 1 | 118 | 468 | 1,976 | 3 | |
| 2 | 2,172 | 13,608 | 18,095 | 6 | |
| 3 | 18,292 | 144,630 | 41,728 | 10 | |
| 4 | 99,535 | 910,872 | 111,563 | 14 | |
| 5 | 408,366 | 4,138,848 | 185,928 | 20 | |
| 6 | 1,373,026 | 15,015,264 | 285,106 | 25 | |
| 7 | 3,979,348 | 46,167,582 | 414,835 | 33 | |
| 8 | 10,276,461 | 125,012,862 | 740,276 | 39 |
The table below gives the times taken to construct the models. There are two stages. Firstly, the system description (in our module based language) is parsed and converted to the MTBDD representing it. Secondly, reachability is performed to identify non-reachable states and the MTBDD is filtered accordingly. Reachability is performed using a BDD based fixpoint algorithm. The number of iterations for this process is also given.
| N | Time (s) | Iter.s | |
| 1 | 0.093 | 19 | |
| 2 | 0.392 | 25 | |
| 3 | 1.297 | 34 | |
| 4 | 7.775 | 44 | |
| 5 | 19.29 | 54 | |
| 6 | 41.64 | 64 | |
| 7 | 89.54 | 74 | |
| 8 | 217.3 | 84 |
We analyse this pathway through the following properties:
These property can be computed by the CSL through the following formulae:
const double t; // time bound // the expected amount of activated MAPK at time t R{"activated"}=?[ I=t ] // the expected amount squared of activated MAPK at time t (used to calculate standard deviation) R{"activated_squared"}=?[ I=t ] // the expected percentage of activated MAPK at time t R{"percentage"}=?[ I=t ] //the expected number of reactions between MAPK and MAKK by time t R{"reactions"}=?[ C<=t ] // the expected time until all MAPK are activated at the same time instant R{"time"}=?[F kpp=N ]
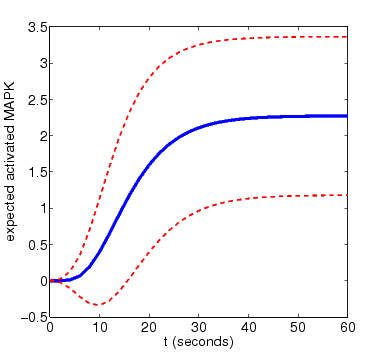
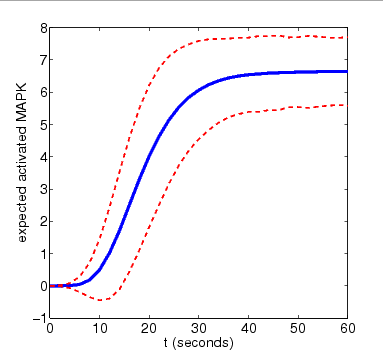
The amount of activated MAPK at time t and the standard deviation of this random variable.
In the graph below, we have plotted this measure as t varies for N=4 and N=8. The graphs also include the standard deviation of the random variable for the amount of activated MAPK at time t, drawn as a pair of dotted lines
N=4
N=8
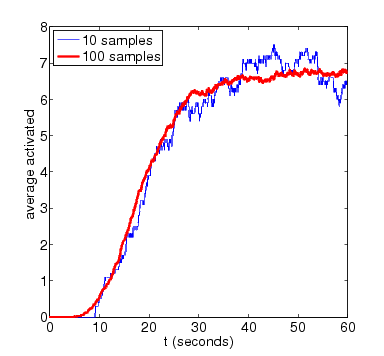
For the purposes of comparison, we also show results for the expected amount of activated MAPK computed using PRISM's discrete-event simulation engine. These are generated using very small numbers of simulation runs (10 and 100). Smoother approximations for the plots above can be obtained with higher numbers of runs.
N=4

N=8
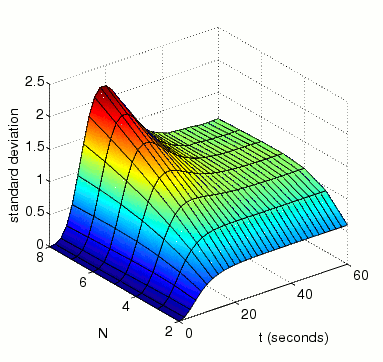
In the graph below we have ploted how the standard deviation of the random variable for the amount of activated MAPK at time t changes as both t and N vary
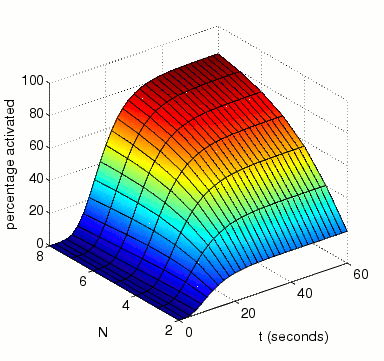
The expected percentage of activated MAPK at time t.
In the graph below, we have plotted this measure as both t and N vary.
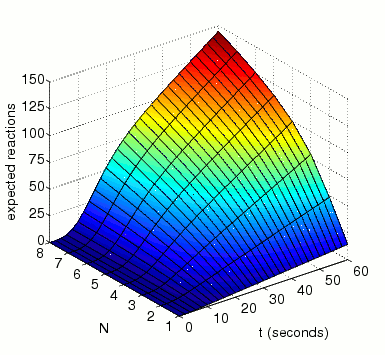
The expected number of reactions between MAPK and MAKK by time t.
In the graph below, we have plotted this measure as both t and N vary.
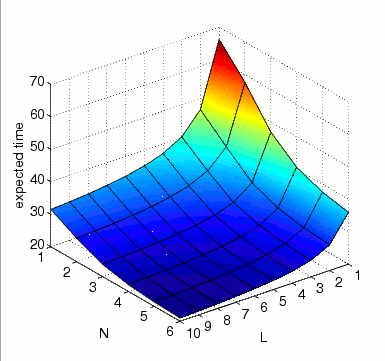
the expected time until all MAPK are activated at the same time instant.
In the graph below we present the results obtained for this property as both N and L vary.