Related publications: [KNP08d]
Gossip protocols are a class of communication protocols which, inspired by the way that gossiping propagates messages in social networks, disseminate content through a network based on periodic exchanges of data with random members of the network. These techniques are designed to function robustly and efficiently on networks that are large, heterogeneous and dynamic in nature. They are hence becoming increasingly important due to the prevalence of, for example, mobile ad-hoc networks, wireless sensor networks and peer-to-peer technologies.
Gossip-based protocols require each node of the system to periodically exchange information with a number of its peers. The choice of which peers nodes communicate with is crucial to how information gets disseminated through the network. Theoretically, a node could randomly select a subset of all the available nodes in the network. In practice, however, this is not feasible since it would require each node to store a complete network membership table which is expensive to store and maintain. In this case study we consider the peer sampling framework of [JGKS07] where each node instead maintains a relatively small local membership table providing a partial view of the network which is periodically updated using a gossiping procedure.
We assume a network of N nodes, each with an address that is required for sending a message to it (as in, for example, a wireless network). Each node maintains a partial view of the network: a list of up to c (<N) node descriptors, each of which comprises a node's network address and an age that represents the freshness of the descriptor.
Periodically each node will execute a gossiping algorithm which exchanges the information contained in their views. This allows information about the topology of the network (and changes to it) to be propagated between nodes. The fundamental idea behind gossip-based protocols is that each node passes information to a small, random subset of the other nodes. This prevents overloading of the network with large numbers of superfluous messages.
The framework of [JGKS07] includes a number of design choices regarding the gossip protocol. For example peer selection, which is the choice of a node to exchange views with, can be done at random or by selecting the node in the view with the oldest age. We will assume a random choice. Several strategies also exist for view propagation, which defines how two nodes exchange their views, e.g. push or pushpull: one- or two-way exchange of views between the sending and receiving node. We assume that the sending node pushes the whole of its view to the receiving node. Finally, the receiving node requires a strategy for view selection, which combines the incoming and the existing view information. In our model, we in fact use hop-counts as a coarse (bounded) measure of the age of each node descriptor. A receiving node increments the the hop-count of all the incoming descriptors, merges these with the descriptors in its own view (keeping the entry with the youngest count in cases of duplication) and then keeps the c newest entries from the combined set.
With regards to the timing of the protocol, we assume that the exchange of data between nodes occurs periodically (with some fixed period) and that each node sends its data exactly once in each round of execution. Such a scheme can be achieved in practice through synchronisation of local clocks. Due to the distributed nature of the system, however, the order in which the nodes participate in each round is unknown (and may be different each time).
The gossip protocol therefore exhibits both probabilistic behaviour (random peer selection) and nondeterministic behaviour (scheduling of nodes within a round) and is naturally modelled as a Markov decision process (MDP).
We opt to build a small, but detailed, model of the system. The model comprises several components: one for for each node in the network and one representing a scheduler who chooses (nondeterministically) the order in which nodes execute the protocol. The state of each node in the network includes its current view, information about which part of the protocol it is currently executing and a buffer to store incoming data from other nodes. The scheduler simply keeps track of which nodes have sent data in the current round. For simplicity, we assume that the sending and updating of views is an atomic step, i.e. throughout the process of one node sending its view to another, no other communication occurs in the network.
Because of the detailed nature of the model and the corresponding state space size, we consider only very small sizes of network (N=3,4) and fix a local view size of c=2. It is possible, though, that anomalies observed in these small models will also be exhibited by networks of a more realistic size. As regards the initial configuration of the model (i.e. the initial local views of each node), we assume that one node is `public' and that all other nodes know the address of this node (but it is not aware of the others). This configuration is suitably realistic and ensures that a connected network is possible.
The PRISM model for the four node network is given below.
// Gossip protocol based on // M. Jelasity and S. Voulgaris and R. Guerraoui and A. Kermarrec and M. van Steen}, // Gossip-based peer sampling, ACM Trans. Computer Systems, 25(3), 2007 // dxp/gxn 04/07/2008 // N=4 (four nodes) // c=2 (size of view equals two) // view propagation policy: push // view selection policy: head (since store entries according to age) // and use hopcount as a coarse bound for age // FULL ATOMICITY - only one message concurrently (reduces interleaving) // ---------------------------------------------------------------------------- // CONSTANTS const int N = 4; // number of nodes const int id1 = 1; // id for node 1 const int id2 = 2; // id for node 2 const int id3 = 3; // id for node 3 const int id4 = 4; // id for node 4 // formula used for updating views formula already_have_addr1 = a1=v1_1_a | a1=v1_2_a; // new address already in view formula already_have_lower1 = (a1=v1_1_a & h1+1>=v1_1_h) | (a1=v1_2_a & h1+1>=v1_2_h); // address has lower hop count in current view formula where_to_put1 = h1+1<=v1_1_h?1:h1+1<=v1_2_h?2:3; // where the new entry should be put in the view formula size_of_view1 = (v1_1_a>0?1:0) + (v1_2_a>0?1:0); // number of entries in a nodes view // ---------------------------------------------------------------------------- // initial views of the nodes // initial view of node 1 (can see 2 one hop away) const int iv1_1_a = 2; const int iv1_2_a = 0; const int iv1_1_h = 1; const int iv1_2_h = 4; // initial view of node 2 (empty) const int iv2_1_a = 0; const int iv2_2_a = 0; const int iv2_1_h = 4; const int iv2_2_h = 4; // initial view of node 3 (can see 2 one hop away) const int iv3_1_a = 2; const int iv3_2_a = 0; const int iv3_1_h = 1; const int iv3_2_h = 4; // initial view of node 4 (can see 2 one hop away) const int iv4_1_a = 2; const int iv4_2_a = 0; const int iv4_1_h = 1; const int iv4_2_h = 4; // ---------------------------------------------------------------------------- // scheduler nondeterministically chooses which node to schedule next in the current round // note each node is only scheduled one in a round module SCHED b1 : [0..1]; // node 1 has been scheduled b2 : [0..1]; // node 2 has been scheduled b3 : [0..1]; // node 3 has been scheduled b4 : [0..1]; // node 4 has been scheduled [start1] b1=0 & (b2+b3+b4<3) -> (b1'=1); // schedule node 1 and stay in current round [start2] b2=0 & (b1+b3+b4<3) -> (b2'=1); // schedule node 2 and stay in current round [start3] b3=0 & (b1+b2+b4<3) -> (b3'=1); // schedule node 3 and stay in current round [start4] b4=0 & (b1+b2+b3<3) -> (b4'=1); // schedule node 4 and stay in current round [start1] b1=0 & (b2+b3+b4=3) -> (b1'=0) & (b2'=0) & (b3'=0) & (b4'=0); // schedule node 1 move to next round [start2] b2=0 & (b1+b3+b4=3) -> (b1'=0) & (b2'=0) & (b3'=0) & (b4'=0); // schedule node 2 move to next round [start3] b3=0 & (b1+b2+b4=3) -> (b1'=0) & (b2'=0) & (b3'=0) & (b4'=0); // schedule node 3 move to next round [start4] b4=0 & (b1+b2+b3=3) -> (b1'=0) & (b2'=0) & (b3'=0) & (b4'=0); // schedule node 4 move to next round endmodule // ---------------------------------------------------------------------------- // module for node 1 module M1 s1 : [0..3]; // View, comprising c address/hop-count pairs // (implicitly, also store fact that our own hop count is 0) v1_1_a : [0..4] init iv1_1_a; v1_2_a : [0..4] init iv1_2_a; v1_1_h : [0..4] init iv1_1_h; v1_2_h : [0..4] init iv1_2_h; // variables to store the information received before it is merged with the view a1 : [0..4]; // address h1 : [0..4]; // hop count i1 : [0..2]; // who sent it // Who we are currently sending data to (0 = nobody) send1: [0..N]; // RECEIVING ----------------------------------------------------- // Receive first new address/hop-count pair [push2_1_0] s1=0 -> (s1'=1) & (a1'=id2) & (h1'=0); [push3_1_0] s1=0 -> (s1'=1) & (a1'=id3) & (h1'=0); [push4_1_0] s1=0 -> (s1'=1) & (a1'=id4) & (h1'=0); // Receive subsequent address/hop-count pair from same sender [push2_1_1] s1=0 -> (s1'=1) & (a1'=v2_1_a) & (h1'=v2_1_h); [push3_1_1] s1=0 -> (s1'=1) & (a1'=v3_1_a) & (h1'=v3_1_h); [push4_1_1] s1=0 -> (s1'=1) & (a1'=v4_1_a) & (h1'=v4_1_h); // (or receive notification that this is the end of the pairs being sent) [push2_1_end] s1=0 -> (s1'=0) & (a1'=0) & (h1'=0); [push3_1_end] s1=0 -> (s1'=0) & (a1'=0) & (h1'=0); [push4_1_end] s1=0 -> (s1'=0) & (a1'=0) & (h1'=0); // Received hop count is for this process so discard (will always be > 0) [] s1=1 & a1=id1 -> (s1'=0) & (a1'=0) & (h1'=0); // Received hop count for address for which we already have a lower hop count so discard [] s1=1 & !(a1=id1) & already_have_lower1 -> (s1'=0) & (a1'=0) & (h1'=0); // Received hop count for address for which we already have a value but new one is lower // (need to store new pair in position "where_to_put1" and shift some pairs to the right) // (i.e.: pairs at position i for which i>=where_to_put1 and i<position of old value) // Old value stored in position 1 [] s1=1 & !(a1=id1) & a1=v1_1_a & h1+1<v1_1_h -> (s1'=0) & (v1_1_h'=h1+1) & (a1'=0) & (h1'=0); // Old value stored in position 2 [] s1=1 & !(a1=id1) & !(a1=v1_1_a) & a1=v1_2_a & h1+1<v1_2_h & where_to_put1=2 -> (s1'=0) & (v1_2_a'=a1) & (v1_2_h'=h1+1) & (a1'=0) & (h1'=0); [] s1=1 & !(a1=id1) & !(a1=v1_1_a) & a1=v1_2_a & h1+1<v1_2_h & where_to_put1=1 -> (s1'=0) & (v1_1_a'=a1) & (v1_1_h'=h1+1) & (v1_2_a'=v1_1_a) & (v1_2_h'=v1_1_h) & (a1'=0) & (h1'=0); // Received hop count for address for which we have no existing value // (need to shift existing pair one to the right) [] s1=1 & !(a1=id1 | already_have_addr1) & where_to_put1=3 -> (s1'=0) & (a1'=0) & (h1'=0); [] s1=1 & !(a1=id1 | already_have_addr1) & where_to_put1=2 -> (s1'=0) & (v1_2_a'=a1) & (v1_2_h'=h1+1) & (a1'=0) & (h1'=0); [] s1=1 & !(a1=id1 | already_have_addr1) & where_to_put1=1 -> (s1'=0) & (v1_1_a'=a1) & (v1_1_h'=h1+1) & (v1_2_a'=v1_1_a) & (v1_2_h'=v1_1_h) & (a1'=0) & (h1'=0); // SENDING ----------------------------------------------------- // start sending when scheduled [start1] s1=0 & !(s2>0 | s3>0 | s4>0) -> (s1'=2); //decide what needs to be sent [] s1=2 & size_of_view1=0 -> (s1'=0); [] s1=2 & size_of_view1=1 -> (s1'=3) & (send1'=v1_1_a); [] s1=2 & size_of_view1=2 -> 0.5 : (s1'=3) & (send1'=v1_1_a) + 0.5 : (s1'=3) & (send1'=v1_2_a); // send to node 2 [push1_2_0] s1=3 & send1=id2 & i1=0 -> (i1'=i1+1); [push1_2_1] s1=3 & send1=id2 & i1=1 & v1_1_h<4 -> (s1'=0) & (i1'=0) & (send1'=0); [push1_2_end] s1=3 & send1=id2 & ((i1=1&v1_1_h=4) | (i1=2&v1_2_h=4)) -> (s1'=0) & (i1'=0) & (send1'=0); // send to node 3 [push1_3_0] s1=3 & send1=id3 & i1=0 -> (i1'=i1+1); [push1_3_1] s1=3 & send1=id3 & i1=1 & v1_1_h<4 -> (s1'=0) & (i1'=0) & (send1'=0); [push1_3_end] s1=3 & send1=id3 & ((i1=1&v1_1_h=4) | (i1=2&v1_2_h=4)) -> (s1'=0) & (i1'=0) & (send1'=0); // send to node 4 [push1_4_0] s1=3 & send1=id4 & i1=0 -> (i1'=i1+1); [push1_4_1] s1=3 & send1=id4 & i1=1 & v1_1_h<4 -> (s1'=0) & (i1'=0) & (send1'=0); [push1_4_end] s1=3 & send1=id4 & ((i1=1&v1_1_h=4) | (i1=2&v1_2_h=4)) -> (s1'=0) & (i1'=0) & (send1'=0); endmodule // ---------------------------------------------------------------------------- // Renamings: Process j>1 is the same as process 1 but with roles of process 1/j swapped module M2 = M1 [ id1=id2, id2=id1, s1=s2, s2=s1, h1=h2, a1=a2, i1=i2, send1=send2, send2=send1, start1=start2, v1_1_a=v2_1_a, v1_2_a=v2_2_a, v1_1_h=v2_1_h, v1_2_h=v2_2_h, v2_1_a=v1_1_a, v2_2_a=v1_2_a, v2_1_h=v1_1_h, v2_2_h=v1_2_h, iv1_1_a=iv2_1_a, iv1_2_a=iv2_2_a, iv1_1_h=iv2_1_h, iv1_2_h=iv2_2_h, push1_2_0=push2_1_0, push1_2_1=push2_1_1, push1_2_2=push2_1_2, push1_2_3=push2_1_3, push1_2_end=push2_1_end, push1_3_0=push2_3_0, push1_3_1=push2_3_1, push1_3_2=push2_3_2, push1_3_3=push2_3_3, push1_3_end=push2_3_end, push1_4_0=push2_4_0, push1_4_1=push2_4_1, push1_4_2=push2_4_2, push1_4_3=push2_4_3, push1_4_end=push2_4_end, push2_1_0=push1_2_0, push2_1_1=push1_2_1, push2_1_2=push1_2_2, push2_1_3=push1_2_3, push2_1_end=push1_2_end, push3_1_0=push3_2_0, push3_1_1=push3_2_1, push3_1_2=push3_2_2, push3_1_3=push3_2_3, push3_1_end=push3_2_end, push4_1_0=push4_2_0, push4_1_1=push4_2_1, push4_1_2=push4_2_2, push4_1_3=push4_2_3, push4_1_end=push4_2_end ] endmodule module M3 = M1 [ id1=id3, id3=id1, s1=s3, s3=s1, h1=h3, a1=a3, i1=i3, send1=send3, send3=send1, start1=start3, v1_1_a=v3_1_a, v1_2_a=v3_2_a, v1_1_h=v3_1_h, v1_2_h=v3_2_h, v3_1_a=v1_1_a, v3_2_a=v1_2_a, v3_1_h=v1_1_h, v3_2_h=v1_2_h, iv1_1_a=iv3_1_a, iv1_2_a=iv3_2_a, iv1_1_h=iv3_1_h, iv1_2_h=iv3_2_h, push1_2_0=push3_2_0, push1_2_1=push3_2_1, push1_2_2=push3_2_2, push1_2_3=push3_2_3, push1_2_end=push3_2_end, push1_3_0=push3_1_0, push1_3_1=push3_1_1, push1_3_2=push3_1_2, push1_3_3=push3_1_3, push1_3_end=push3_1_end, push1_4_0=push3_4_0, push1_4_1=push3_4_1, push1_4_2=push3_4_2, push1_4_3=push3_4_3, push1_4_end=push3_4_end, push2_1_0=push2_3_0, push2_1_1=push2_3_1, push2_1_2=push2_3_2, push2_1_3=push2_3_3, push2_1_end=push2_3_end, push3_1_0=push1_3_0, push3_1_1=push1_3_1, push3_1_2=push1_3_2, push3_1_3=push1_3_3, push3_1_end=push1_3_end, push4_1_0=push4_3_0, push4_1_1=push4_3_1, push4_1_2=push4_3_2, push4_1_3=push4_3_3, push4_1_end=push4_3_end ] endmodule module M4 = M1 [ id1=id4, id4=id1, s1=s4, s4=s1, h1=h4, a1=a4, i1=i4, send1=send4, send4=send1, start1=start4, v1_1_a=v4_1_a, v1_2_a=v4_2_a, v1_1_h=v4_1_h, v1_2_h=v4_2_h, v4_1_a=v1_1_a, v4_2_a=v1_2_a, v4_1_h=v1_1_h, v4_2_h=v1_2_h, iv1_1_a=iv4_1_a, iv1_2_a=iv4_2_a, iv1_1_h=iv4_1_h, iv1_2_h=iv4_2_h, push1_2_0=push4_2_0, push1_2_1=push4_2_1, push1_2_2=push4_2_2, push1_2_3=push4_2_3, push1_2_end=push4_2_end, push1_3_0=push4_3_0, push1_3_1=push4_3_1, push1_3_2=push4_3_2, push1_3_3=push4_3_3, push1_3_end=push4_3_end, push1_4_0=push4_1_0, push1_4_1=push4_1_1, push1_4_2=push4_1_2, push1_4_3=push4_1_3, push1_4_end=push4_1_end, push2_1_0=push2_4_0, push2_1_1=push2_4_1, push2_1_2=push2_4_2, push2_1_3=push2_4_3, push2_1_end=push2_4_end, push3_1_0=push3_4_0, push3_1_1=push3_4_1, push3_1_2=push3_4_2, push3_1_3=push3_4_3, push3_1_end=push3_4_end, push4_1_0=push1_4_0, push4_1_1=push1_4_1, push4_1_2=push1_4_2, push4_1_3=push1_4_3, push4_1_end=push1_4_end ] endmodule // ---------------------------------------------------------------------------- // formula needed for computing maximum path length formula max_hop_count = max(v1_1_h,v1_2_h,v2_1_h,v2_2_h,v3_1_h,v3_2_h); formula node_degree1=(v1_1_a>0?1:0)+(v1_2_a>0?1:0); formula n12 = v1_1_a=2|v1_2_a=2; formula n13 = v1_1_a=3|v1_2_a=3; formula n14 = v1_1_a=4|v1_2_a=4; formula n21 = v2_1_a=1|v2_2_a=1; formula n23 = v2_1_a=3|v2_2_a=3; formula n24 = v2_1_a=4|v2_2_a=4; formula n31 = v3_1_a=1|v3_2_a=1; formula n32 = v3_1_a=2|v3_2_a=2; formula n34 = v3_1_a=4|v3_2_a=4; formula n41 = v4_1_a=1|v4_2_a=1; formula n42 = v4_1_a=2|v4_2_a=2; formula n43 = v4_1_a=3|v4_2_a=3; formula path_len12 = n12?1:n13&n32|n14&n42?2:n13&n34&n42|n14&n43&n32?3:4; formula path_len13 = n13?1:n12&n23|n14&n43?2:n12&n24&n43|n14&n42&n23?3:4; formula path_len14 = n14?1:n12&n24|n13&n34?2:n12&n23&n34|n13&n32&n24?3:4; formula max_path_len1=max(path_len12,path_len13,path_len14); formula sum_path_len1=path_len12+path_len13+path_len14; formula path_len21 = n21?1:n23&n31|n24&n41?2:n23&n34&n41|n24&n43&n31?3:4; formula path_len23 = n23?1:n21&n13|n24&n43?2:n21&n14&n43|n24&n41&n13?3:4; formula path_len24 = n24?1:n21&n14|n23&n34?2:n21&n13&n34|n23&n31&n14?3:4; formula max_path_len2=max(path_len21,path_len23,path_len24); formula sum_path_len2=path_len21+path_len23+path_len24; formula path_len32 = n32?1:n31&n12|n34&n42?2:n31&n14&n42|n34&n41&n12?3:4; formula path_len31 = n31?1:n32&n21|n34&n41?2:n32&n24&n41|n34&n42&n21?3:4; formula path_len34 = n34?1:n32&n24|n31&n14?2:n32&n21&n14|n31&n12&n24?3:4; formula max_path_len3=max(path_len32,path_len31,path_len34); formula sum_path_len3=path_len32+path_len31+path_len34; formula path_len42 = n42?1:n43&n32|n41&n12?2:n43&n31&n12|n41&n13&n32?3:4; formula path_len43 = n43?1:n42&n23|n41&n13?2:n42&n21&n13|n41&n12&n23?3:4; formula path_len41 = n41?1:n42&n21|n43&n31?2:n42&n23&n31|n43&n32&n21?3:4; formula max_path_len4=max(path_len42,path_len43,path_len41); formula max_path_len=max(max_path_len1,max_path_len2,max_path_len3,max_path_len4); // ---------------------------------------------------------------------------- // REWARDS // maximum path length rewards "max_path_len" true : max_path_len; endrewards // maximum path length squared (for computing variance) rewards "max_path_len_sq" true : max_path_len*max_path_len; endrewards // rounds rewards "rounds" [start1] b1+b2+b3+b4=3 : 1; [start2] b1+b2+b3+b4=3 : 1; [start3] b1+b2+b3+b4=3 : 1; [start4] b1+b2+b3+b4=3 : 1; endrewards
We analyse the performance of the gossip protocol concentrating on how the topology of the network induced by the local views of the nodes varies over time. More precisely, we investigate:
For the former, we demonstrate an analysis of the best- and worst-case behaviour of the model, and how this relates to the average case. For the latter, we show how obtaining best and worst-case adversaries (schedulers) of the MDP can help to identify the scenarios in which the best and worst cases occur.
These property can be computed by PRISM through the following formulae:
const int T; // time bound // maximum path length at time T R{"max_path_len_sq"}min=?[I=T] // minimum under all schedulers R{"max_path_len_sq"}max=?[I=T] // maximum under all schedulers R{"max_path_len_sq"}=?[I=T] // for DTMC model // to get the variance plots for the maximum path length (dtmc model) R{"max_path_len"}=?[I=T]+pow(R{"max_path_len_sq"}=?[I=T]-pow(R{"max_path_len"}=?[I=T],2), 0.5) R{"max_path_len"}=?[I=T]-pow(R{"max_path_len_sq"}=?[I=T]-pow(R{"max_path_len"}=?[I=T],2), 0.5) // states where network is connected label "done" = max_path_len<4; // minimum and maximum probability nodes become connected Pmin=? [ F<=T "done" ] Pmax=? [ F<=T "done" ] // minimum and maximum expected number of rounds until connected R{"rounds"}min=? [ F "done" ] R{"rounds"}max=? [ F "done" ]
The maximum path length (longest route between nodes).
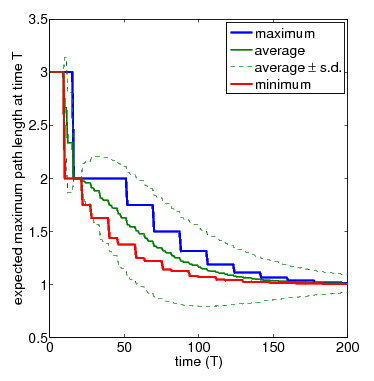
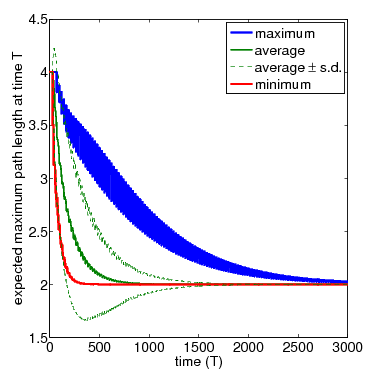
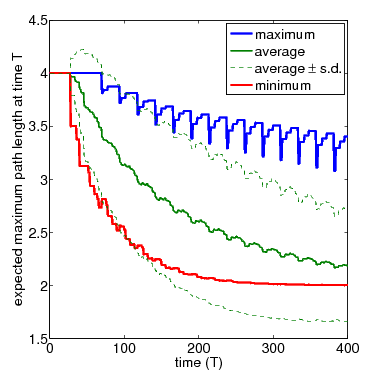
In the graph below, show the full set of these results for N=3 and N=4 nodes, respectively. The thicker solid lines show the minimum and maximum expected longest path length after T time-steps, for a range of values of T. In between these, the thinner solid line shows the average (i.e. expected) value for the same time points. The dashed lines indicate the standard deviation. The average values can be calculated by replacing the nondeterminism in the scheduler component of the PRISM model with uniform probabilistic choices, yielding a DTMC instead of an MDP. While the standard deviation is computed through the reward structure max_path_len_sq and the equivalence
See the properties file above for further details.
N=3
N=4
N=4 (zoom)
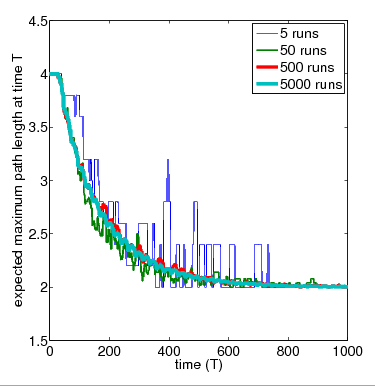
For the purposes of comparison, below we have included the average results over 5, 50, 500 and 5,000 simulation runs for the network of 4 nodes obtained with PRISM's discrete-event simulation engine.
The time for the network to become connected.
We compute the (minimum and maximum) expected number of complete gossiping rounds required before the combined views of the nodes generate a connected network. This is a desirable configuration for the network to reach since, when the local views do not form a connected topology, the nodes have insufficient information to ensure that a message gets propagated to all other nodes in the network.
As well as computing these measures, we use a prototype extension of PRISM to generate actual adversaries that result in the minimum and maximum values. Since the only nondeterminism in the model is due to scheduling of the nodes (i.e. the order in which they forward their views to their neighbours), we can extract from an adversary the corresponding scheduling.
N=3.
In the case of three nodes, the minimum and maximum number of complete rounds required for the local views to generate a connected network is 0 and 1 respectively. For comparison, in the DTMC model, where nondeterminism has been replaced by uniform random choice, the expected number of rounds is 0.667. The figure below illustrates the sequences of node schedulings that result in these minimum and maximum values.
minimum
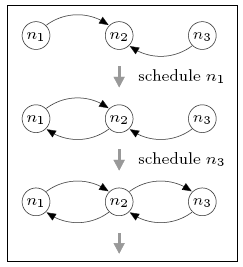
maximum
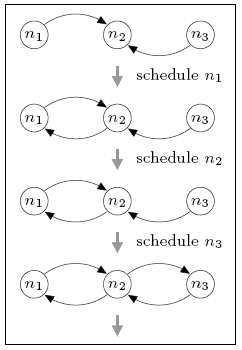
Initially, all nodes can see node n2, but no others. The best-case behaviour (minimum expected number of complete rounds) can be obtained by first scheduling node n1 and then node n3, after which n2 has added both n1 and n3 to its view and the network is connected. Since n2 has yet to be scheduled, the minimum expected number of complete rounds is 0. For worst-case behaviour (maximum value), we can schedule n2 before either n1 or n3 is scheduled. This adds no new information to the local views and means that a complete gossiping round is required before the network becomes connected.
N=4.
For the network consisting of four nodes, we find that the minimum and maximum expected number of complete rounds before connectivity are 1.5 and 4.5 respectively. For comparison, the expected number of rounds for the DTMC model is 2.788 which, unlike in the case of the three node network, is closer to the minimum than the maximum.
This case is more complex than the three node network. Since more than one round may be required before the network becomes connected and the number of possible neighbours exceeds the size of the view, descriptors can be dropped from the views as more recent information becomes available. Furthermore, we must consider a node's choice of who to send data to. The figure below shows part of the scheduling (the first gossiping round) that can result in the minimum and maximum expected number of complete rounds. In both cases notice that, when node n4 is scheduled the view of n2 is updated, causing the removal of n1 (the oldest descriptor). Not also that, when node n2 is scheduled it makes a (random) selection between communicating with n1 or n3 since both are in its view at the time.
minimum
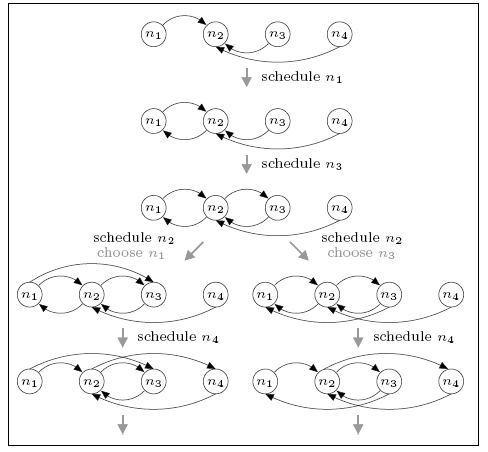
maximum
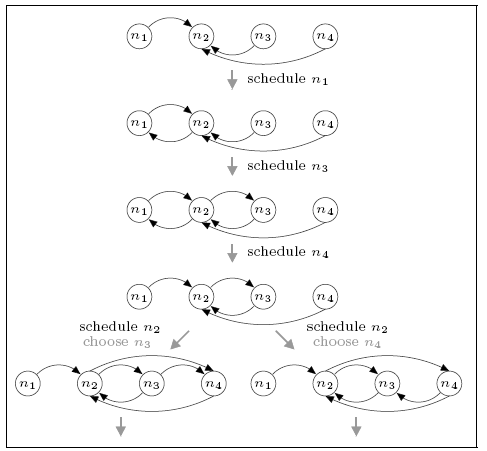
For the minimum case we see that, if n2 chooses to gossip with n3 (i.e. the right-hand branch), then the network is complete by the end of the first round. If it chooses n1 (i.e. the left branch) this is not the case (there are no paths to n1) and further rounds of the protocol are required. This leads to a (minimum) expected number of rounds of 1.5. For the maximum case, the network is not connected under either choice and several further rounds are required.