Workstation Cluster

(Haverkort, Hermanns & Katoen)

Introduction
Model Statistics
Model Construction Times
Steady State Probability Computation
Model Checking

Introduction

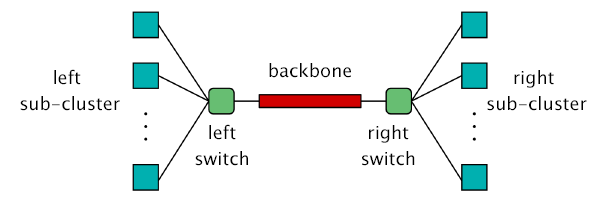
This case study is based on a cluster of workstations, taken from [HHK00]. The system comprises two sub-clusters with N workstations in each, connected in a star topology. The switches connecting each sub-cluster are joined by a central backbone. All components can break down and there is a single repair unit to service all components.

We define two levels of Quality of Service (QoS):

minimum QoS: at least 3N/4 workstations are operational and connected via switches and backbone;
premium QoS: at least N workstations are operational and connected via switches and backbone.

The model is represented as a CTMC. The PRISM source code is given below.

// Workstation cluster [HHK00]
// dxp/gxn 11/01/00

ctmc

const int N; // Number of workstations in each cluster
const int left_mx = N; // Number of work stations in left cluster
const int right_mx = N; // Number of work stations in right cluster

// Minimum QoS requires 3/4 connected workstations operational
const int k = floor(0.75*N);
formula minimum = (left_n>=k & toleft_n) | 
                  (right_n>=k & toright_n) | 
                  ((left_n+right_n)>=k & toleft_n & line_n & toright_n);

// Failure rates
const double ws_fail = 1/500; // Single workstation: average time to fail = 500 hrs
const double switch_fail = 1/4000; // Switch: average time to fail = 4000 hrs
const double line_fail = 1/5000; // Backbone: average time to fail = 5000 hrs

// Left cluster
module Left 
	
	left_n : [0..left_mx] init left_mx; // Number of workstations operational
	left : bool; // Being repaired?
	
	[startLeft] !left & (left_n<left_mx) -> 1 : (left'=true);
	[repairLeft] left & (left_n<left_mx) -> 1 : (left'=false) & (left_n'=left_n+1);
	[] (left_n>0) -> ws_fail*left_n : (left_n'=left_n-1);
	
endmodule

// Right cluster
module Right = Left[left_n=right_n,
                    left=right,
                    left_mx=right_mx,
                    startLeft=startRight,
                    repairLeft=repairRight ]
endmodule

// Repair unit
module Repairman
	
	r : bool; // Repairing?
	
	[startLeft]    !r -> 10 : (r'=true); // Inspect Left 
	[startRight]   !r -> 10 : (r'=true); // Inspect Right 
	[startToLeft]  !r -> 10 : (r'=true); // Inspect ToLeft
	[startToRight] !r -> 10 : (r'=true); // Inspect ToRight 
	[startLine]    !r -> 10 : (r'=true); // Inspect Line 
	
	[repairLeft]    r -> 2     : (r'=false); // Repair Left 
	[repairRight]   r -> 2     : (r'=false); // Repair Right
	[repairToLeft]  r -> 0.25  : (r'=false); // Repair ToLeft
	[repairToRight] r -> 0.25  : (r'=false); // Repair ToRight
	[repairLine]    r -> 0.125 : (r'=false); // Repair Line
	
endmodule

// Line/backbone
module Line 
	
	line :   bool; // Being repaired?
	line_n : bool init true; // Working?
	
	[startLine] !line & !line_n -> 1 : (line'=true);
	[repairLine] line & !line_n -> 1 : (line'=false) & (line_n'=true);
	[] line_n -> line_fail : (line_n'=false);
	
endmodule

// Left switch
module ToLeft = Line[line=toleft,
                     line_n=toleft_n,
                     line_fail=switch_fail,
                     startLine=startToLeft,
                     repairLine=repairToLeft ]
endmodule

// Right switch
module ToRight = Line[line=toright,
                      line_n=toright_n,
                      line_fail=switch_fail,
                      startLine=startToRight,
                      repairLine=repairToRight ]
endmodule

// Reward structures

// Percentage of operational workstations stations
rewards "percent_op"
	true : 100*(left_n+right_n)/(2*N);
endrewards

// Time that the system is not delivering at least minimum QoS
rewards "time_not_min"
	!minimum : 1; 
endrewards

// Number of repairs
rewards "num_repairs"
	[repairLeft]    true : 1;
	[repairRight]   true : 1;
	[repairToLeft]  true : 1;
	[repairToRight] true : 1;
	[repairLine]    true : 1;
endrewards

View: printable version Download: cluster.sm

Model Statistics

The table below shows statistics for each model we have built. The first section gives information about the CTMC representing the model: the number of states and the number of non zeros (transitions). The second part refers to the MTBDD which represents this CTMC: the total number of nodes, the number of leaves (terminal nodes), and the amount of memory needed to store it. The last column gives the amount of memory a sparse matrix would need to represent the same CTMC.

N:	Model:		MTBDD:			Sparse:
N:	States:	NNZ:	Nodes:	Leaves:	Kb:	Kb:
2	276	1,120	331	9	6.46	16.4
4	820	3,616	535	11	10.5	51.9
8	2,772	12,832	968	15	18.9	183
16	10,132	48,160	1,899	23	37.1	683
32	38,676	186,400	3,906	39	76.3	2,637
64	151,060	733,216	8,225	71	160	10,362
128	597,012	2,908,192	17,481	134	341	41,076
256	2,373,652	1.15e+7	37,272	262	728	162,581
512	9,465,876	4.6e+7	79,399	518	1,550	649,990

Model Construction Times

The table below gives the times taken to construct the models. This process involves first building a CTMC (represented as an MTBDD) from the system description (in our module based language), and then computing the reachable states using a BDD based fixpoint algorithm. The total time required and the number of fixpoint iterations are given below.

N:	Construction:
N:	Time (s):	Iter.s:
2	0.14	9
4	0.15	13
8	0.20	21
16	0.05	37
32	0.12	69
64	1.65	133
128	6.20	261
256	23.43	517
512	100.96	1,029

Steady-State Probability Computation

The table below gives the times taken to compute the steady-state probabilities using the JOR method. The number of iterations required and the time taken using the MTBDD, sparse and hybrid engines is as follows.

N:	Time per iteration: (s)			Iterations:
N:	MTBDD	Sparse	Hybrid	Iterations:
2	0.028	0.00026	0.00027	39
4	0.052	0.00031	0.00063	64
8	0.21	0.00085	0.0022	82
16	0.78	0.0035	0.0072	141
32	2.81	0.014	0.025	260
64	9.38	0.14	0.16	540
128	32.6	0.39	0.49	1,276
256	-	-	2.16	3,634
512	-	-	8.99	30,476

The steady-state probabilities allows use to compute properties such as:

S=? [ "premium" ]: the long-run probability that premium QoS will be delivered.
S=? [ !"minimum" ]: the long-run probability that QoS is below minimum.

Model Checking

We have model checked the following properties:

"The system will always be able to offer premium QoS at some point in the future." The corresponding CSL formula is given by:
P>=1 [ true U "premium" ]
Model checking times:

N: Prob1 precomputation:

Time (s): Iterations:

2 0.063 18

4 0.075 26

8 0.073 42

16 0.192 74

32 0.360 138

64 1.27 266

128 3.30 522

256 12.1 1034

512 44.3 2058

Conclusion: the property holds in all states
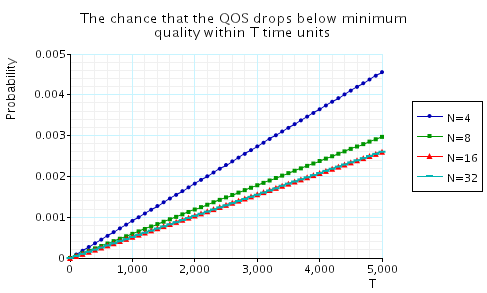
"The chance that the QoS drops below minimum quality within T time units." The corresponding CSL formula is given by
P=? [ true U<=T !"minimum" ]
In the graph below we have plotted these probabilities from a range of values of T and N.
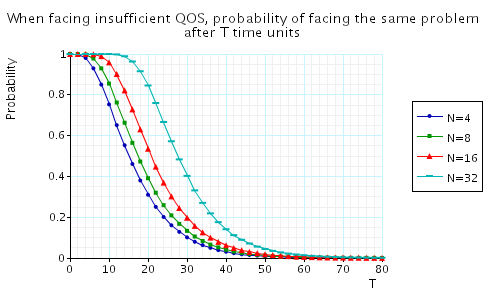
"When facing insufficient QoS, the (maximum) probability of facing the same problem after T time units." The corresponding CSL formula is given by
P=? [ true U[T,T] !"minimum" {!"minimum"}{max} ]
In the graph below we have plotted these probabilities from a range of values of T and N.
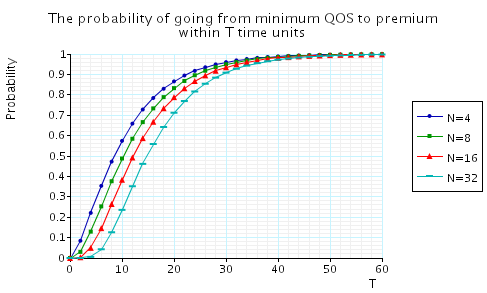
"The probability of going from minimum QoS to premium QoS within T time units." The corresponding CSL formula is given by
P=? [ true U<=T "premium" {"minimum"}{min} ]
In the graph below we have plotted these probabilities from a range of values of T and N.
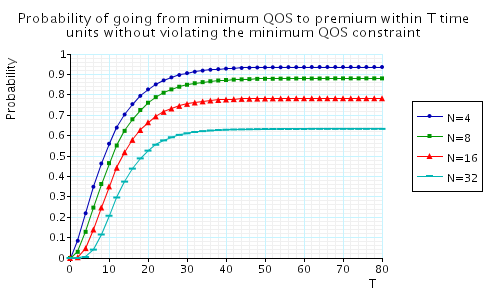
"The probability of going from minimum QoS to premium QoS within T time units without violating the minimum QoS constraint along the way." The corresponding CSL formula is given by
P=? [ "minimum" U<=T "premium" {"minimum"}{min}]
In the graph below we have plotted these probabilities from a range of values of T and N.
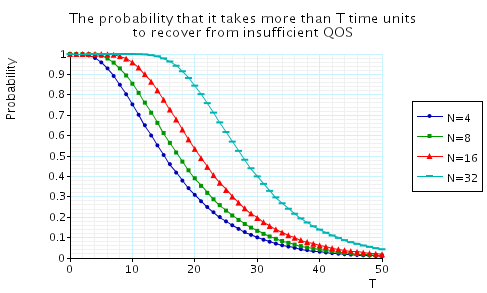
"The probability that it takes more than T time units to recover from insufficient QoS." The corresponding CSL formula is given by
P=? [ !"minimum" U>=T "minimum" {!"minimum"}{max} ]
In the graph below we have plotted these probabilities from a range of values of T and N.
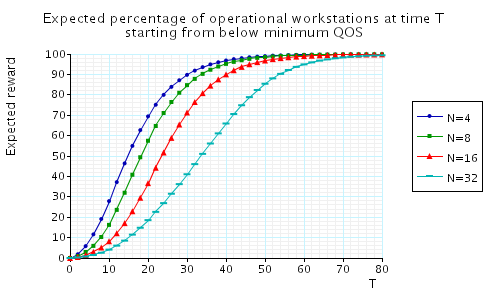
"The minimum percentage of operational workstations at time T when starting from below minimum QoS." The corresponding CSL formula is given by
R{"percent_op"}=?[ I=T {!"minimum"}{min} ]
In the graph below we have plotted these results from a range of values of T and N.
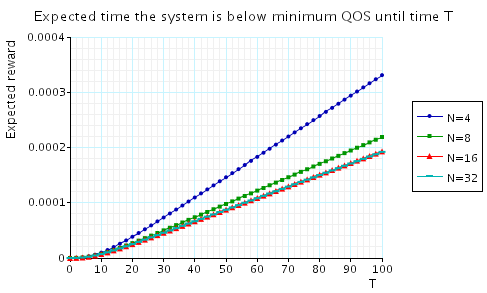
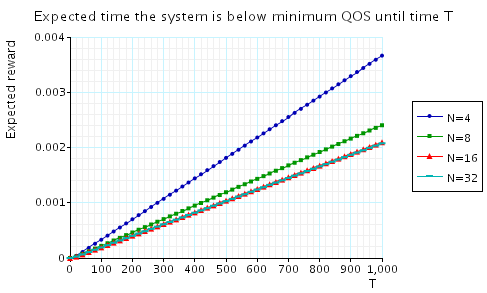
"The expected time that the system is below minimum QoS until time T." The corresponding CSL formula is given by
R{"time_not_min"}=?[ C<=T ]
In the graph below we have plotted these results from a range of values of T and N.
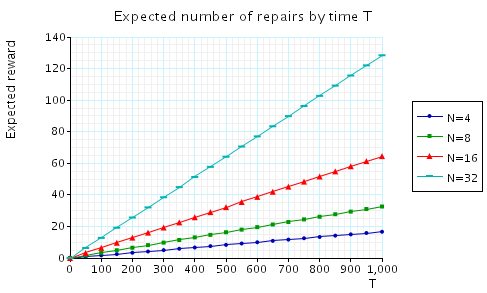
"The expected number of repairs by time T." The corresponding CSL formula is given by
R{"num_repairs"}=?[ C<=T ]
In the graph below we have plotted these results from a range of values of T and N.