Bounded Retransmission Protocol

(D'Argenio, Jeannet, Jensen & Larsen)

Introduction
Model Statistics
Model Construction Times
Model Checking

Introduction

This case study is based on the bounded retransmission protocol (BRP) [HSV94], a variant of the alternating bit protocol. The BRP protocol sends a file in a number of chunks, but allows only a bounded number of retransmissions of each chunk. The model is represented as an MDP. We let N denote the number of chunks and MAX the maximum allowed number of retransmissions of each chunk. The PRISM source code is given below.

// bounded retransmission protocol [D'AJJL01]
// gxn/dxp 23/05/2001

mdp

// number of chunks
const int N;
// maximum number of retransmissions
const int MAX;

module sender

	s : [0..6];
	// 0 idle
	// 1 next_frame	
	// 2 wait_ack
	// 3 retransmit
	// 4 success
	// 5 error
	// 6 wait sync
	srep : [0..3];
	// 0 bottom
	// 1 not ok (nok)
	// 2 do not know (dk)
	// 3 ok (ok)
	nrtr : [0..MAX];
	i : [0..N];
	bs : bool;
	s_ab : bool;
	fs : bool;
	ls : bool;
	
	// idle
	[NewFile] (s=0) -> (s'=1) & (i'=1) & (srep'=0);
	// next_frame
	[aF] (s=1) -> (s'=2) & (fs'=(i=1)) & (ls'=(i=N)) & (bs'=s_ab) & (nrtr'=0);
	// wait_ack
	[aB] (s=2) -> (s'=4) & (s_ab'=!s_ab);
	[TO_Msg] (s=2) -> (s'=3);
	[TO_Ack] (s=2) -> (s'=3);
	// retransmit
	[aF] (s=3) & (nrtr<MAX) -> (s'=2) & (fs'=(i=1)) & (ls'=(i=N)) & (bs'=s_ab) & (nrtr'=nrtr+1);
	[] (s=3) & (nrtr=MAX) & (i<N) -> (s'=5) & (srep'=1);
	[] (s=3) & (nrtr=MAX) & (i=N) -> (s'=5) & (srep'=2);
	// success
	[] (s=4) & (i<N) -> (s'=1) & (i'=i+1);
	[] (s=4) & (i=N) -> (s'=0) & (srep'=3);
	// error
	[SyncWait] (s=5) -> (s'=6); 
	// wait sync
	[SyncWait] (s=6) -> (s'=0) & (s_ab'=false); 
	
endmodule

module receiver

	r : [0..5];
	// 0 new_file
	// 1 fst_safe
	// 2 frame_received
	// 3 frame_reported
	// 4 idle
	// 5 resync
	rrep : [0..4];
	// 0 bottom
	// 1 fst
	// 2 inc
	// 3 ok
	// 4 nok
	fr : bool;
	lr : bool;
	br : bool;
	r_ab : bool;
	recv : bool;
	
	
	// new_file
	[SyncWait] (r=0) -> (r'=0);
	[aG] (r=0) -> (r'=1) & (fr'=fs) & (lr'=ls) & (br'=bs) & (recv'=T);
	// fst_safe_frame
	[] (r=1) -> (r'=2) & (r_ab'=br);
	// frame_received
	[] (r=2) & (r_ab=br) & (fr=true) & (lr=false)  -> (r'=3) & (rrep'=1);
	[] (r=2) & (r_ab=br) & (fr=false) & (lr=false) -> (r'=3) & (rrep'=2);
	[] (r=2) & (r_ab=br) & (fr=false) & (lr=true)  -> (r'=3) & (rrep'=3);
	[aA] (r=2) & !(r_ab=br) -> (r'=4);  
	// frame_reported
	[aA] (r=3) -> (r'=4) & (r_ab'=!r_ab);
	// idle
	[aG] (r=4) -> (r'=2) & (fr'=fs) & (lr'=ls) & (br'=bs) & (recv'=T);
	[SyncWait] (r=4) & (ls=true) -> (r'=5);
	[SyncWait] (r=4) & (ls=false) -> (r'=5) & (rrep'=4);
	// resync
	[SyncWait] (r=5) -> (r'=0) & (rrep'=0);
	
endmodule
	
module checker

	T : bool;
	
	[NewFile] (T=false) -> (T'=false);
	[NewFile] (T=false) -> (T'=true);
	
endmodule

module	channelK

	k : [0..2];
	
	// idle
	[aF] (k=0) -> 0.98 : (k'=1) + 0.02 : (k'=2);
	// sending
	[aG] (k=1) -> (k'=0);
	// lost
	[TO_Msg] (k=2) -> (k'=0);
	
endmodule

module	channelL

	l : [0..2];
	
	// idle
	[aA] (l=0) -> 0.99 : (l'=1) + 0.01 : (l'=2);
	// sending
	[aB] (l=1) -> (l'=0);
	// lost
	[TO_Ack] (l=2) -> (l'=0);
	
endmodule

View: printable version Download: brp.nm

We note that, as in [DJJL01], we have added a checker process which ensures that when checking properties we are only considering the transmission of one file, that is, we are not interested in checking properties after a transmission was successful or unsuccessful.

Model Statistics

The table below shows statistics for each model we have built. The first section gives the number of states in the MDP representing the model. The second part refers to the MTBDD which represents this MDP: the total number of nodes and the number of leaves (terminal nodes).

N:	MAX:	Model:	MTBDD:
N:	MAX:	States:	Nodes:	Leaves:
16	2	1,512	2,938	6
16	3	1,966	2,933	6
16	4	2,420	3,014	6
16	5	2,874	3,002	6

32	2	2,856	3,058	6
32	3	3,726	3,053	6
32	4	4,596	3,134	6
32	5	5,466	3,122	6

64	2	5,544	3,178	6
64	3	7,246	3,173	6
64	4	8,948	3,254	6
64	5	10,650	3,242	6

Model Construction Times

The table below gives the times taken to construct the models. There are two stages. Firstly, the system description (in our module based language) is parsed and converted to the MTBDD representing it. Secondly, reachability is performed to identify non-reachable states and the MTBDD is filtered accordingly. Reachability is performed using a BDD based fixpoint algorithm. The number of iterations for this process is also given.

N:	MAX:	Construction:	Reachability:
N:	MAX:	Time (s):	Time (s):	Iter.s:
16	2	0.35	0.39	114
16	3	0.26	0.41	118
16	4	0.26	0.46	122
16	5	0.26	0.50	126

32	2	0.28	0.76	210
32	3	0.28	0.79	214
32	4	0.29	0.88	218
32	5	0.27	0.91	222

64	2	0.28	1.64	402
64	3	0.29	1.71	406
64	4	0.28	1.78	410
64	5	0.30	1.83	414

Model Checking

The PRISM source code for the properties considered is given below.

// property A of [D'AJJL01]
// the maximum probability that eventually the sender reports a certain unsuccessful transmission but the receiver got the complete file
Pmax=?[ F srep=1 & rrep=3 & recv ]

// property B of [D'AJJL01]
// the maximum probability that eventually the sender reports a certain successful transmission but the receiver did not get the complete file
Pmax=?[ F srep=3 & !(rrep=3) & recv ]

// property 1 of [D'AJJL01]
// the maximum probability that eventually the sender does not report a successful transmission
Pmax=?[ F s=5 & T ]

// property 2 of [D'AJJL01]
// the maximum probability that eventually the sender reports an uncertainty on the success of the transmission
Pmax=?[ F s=5 & T & srep=2 ]

// property 3 of [D'AJJL01]
// the maximum probability that eventually the sender reports an unsuccessful transmission after more than 8 chunks have been sent successfully
Pmax=?[ F s=5 & T & srep=1 & i>8 ]

// property 4 of [D'AJJL01]
// the maximum probability that eventually the receiver does not receive any chunk and the sender tried to send a chunk
Pmax=?[ F !(srep=0) & T & !recv ]

View: printable version Download: brp.pctl

There are two precomputation steps in the model checking procedure involving BDD based fixpoint algorithms: Prob1E and Prob0A which finds those states such that the maximum probability of satisfying the formula is 1 and 0 respectively.

In the main algorithm we stop iterating when the relative error between subsequent iteration vectors is less than 1e-6, that is:

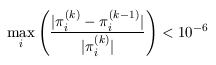
Property A of [DJJL01]: "The maximum probability that eventually the sender reports a certain unsuccessful transmission but the receiver got the complete file."

Model checking times: As in none of the reachable states the sender reports a certain unsuccessful transmission while the receiver got the complete file, the probability of satisfying this property is 0 and model checking reduces to an invariance check.

N: MAX: Time (s):

16 2 0.035

16 3 0.036

16 4 0.040

16 5 0.040

32 2 0.041

32 3 0.042

32 4 0.038

32 5 0.037

64 2 0.038

64 3 0.037

64 4 0.039

64 5 0.040
Property B of [DJJL01]: "The maximum probability that eventually the sender reports a certain successful transmission but the receiver did not get the complete file."

Model checking times: As in none of the reachable states the sender reports a certain unsuccessful transmission while the receiver got the complete file, the probability of satisfying this property is 0 and model checking reduces to an invariance check.

N: MAX: Time (s):

16 2 0.040

16 3 0.038

16 4 0.039

16 5 0.038

32 2 0.041

32 3 0.040

32 4 0.038

32 5 0.041

64 2 0.039

64 3 0.039

64 4 0.041

64 5 0.044

Property 1 of [DJJL01]: "The maximum probability that eventually the sender does not report a successful transmission."

Model checking times:

N:	MAX:	Precomputation:				Main Algorithm:		Probability:
		Prob1E		Prob0A		Time (s):	Iterations:
		Time (s):	Iterations:	Time (s):	Iterations:	Time (s):	Iterations:
16	2	6.44	712	0.14	19	19.72	220	4.23E-4
16	3	7.91	840	0.14	23	25.99	224	1.26E-5
16	4	9.43	968	0.18	27	31.68	226	3.76E-7
16	5	10.81	1,096	0.21	31	36.91	228	1.12E-8

32	2	13.15	1,416	0.12	19	65.96	418	8.46E-4
32	3	15.99	1,672	0.16	23	91.49	422	2.52E-5
32	4	19.34	1,928	0.20	27	111.56	424	7.52E-7
32	5	22.11	2,184	0.22	31	131.87	426	2.24E-8

64	2	27.49	2,824	0.12	19	243.09	812	0.001692
64	3	33.63	3,336	0.15	23	330.06	816	5.05E-5
64	4	40.81	3,848	0.19	27	423.56	818	1.51E-6
64	5	46.28	4,360	0.43	31	511.22	820	4.48E-8

Property 2 of [DJJL01]:"The maximum probability that eventually the sender reports an uncertainty on the success of the transmission."

Model checking times:

N:	MAX:	Precomputation:				Main Algorithm:		Probability:
		Prob1E		Prob0A		Time (s):	Iterations:
		Time (s):	Iterations:	Time (s):	Iterations:	Time (s):	Iterations:
16	2	1.61	234	0.40	110	12.15	224	2.64E-5
16	3	1.75	242	0.43	114	16.09	228	7.89E-7
16	4	1.79	250	0.42	118	14.56	230	2.35E-8
16	5	1.86	258	0.42	122	13.02	232	7.00E-10

32	2	2.84	426	0.67	206	40.40	424	2.64E-5
32	3	2.92	434	0.67	210	53.60	428	7.89E-7
32	4	3.27	442	0.92	214	32.49	430	2.35E-8
32	5	3.29	450	0.97	218	31.88	432	7.00E-10

64	2	5.77	810	2.01	398	146.26	822	2.64E-5
64	3	5.99	818	1.97	402	195.05	824	7.89E-7
64	4	6.17	826	2.07	406	162.18	826	2.35E-8
64	5	6.18	834	2.10	410	90.07	828	7.00E-10

Property 3 of [DJJL01]:"The maximum probability that eventually the sender reports an unsuccessful transmission after more than 8 chunks have been sent successfully."

Model checking times:

N:	MAX:	Precomputation:				Main Algorithm:		Probability:
		Prob1E		Prob0A		Time (s):	Iterations:
		Time (s):	Iterations:	Time (s):	Iterations:	Time (s):	Iterations:
16	2	2.36	342	0.28	68	17.09	216	1.85E-4
16	3	3.22	438	0.30	72	23.06	218	5.52E-6
16	4	4.42	538	0.39	76	30.11	222	1.65E-7
16	5	5.43	642	0.40	80	27.72	224	4.90E-9

32	2	4.49	694	0.36	68	66.38	412	6.08E-4
32	3	5.71	854	0.40	72	89.12	416	1.81E-5
32	4	7.02	1,018	0.61	76	115.14	418	5.41E-7
32	5	8.61	1,186	0.45	80	124.71	420	1.61E-8

64	2	8.25	1,398	0.41	68	253.23	806	0.001454
64	3	10.40	1,686	0.41	72	416.96	810	4.34E-5
64	4	12.98	1,978	0.70	76	449.41	812	1.29E-6
64	5	15.30	2,274	0.49	80	515.21	814	3.85E-8

Property 4 of [DJJL01]: "The maximum probability that eventually the receiver does not receive any chunk and the sender tried to send a chunk."

Model checking times:

N:	MAX:	Precomputation:				Main Algorithm:		Probability:
		Prob1E		Prob0A		Time (s):	Iterations:
		Time (s):	Iterations:	Time (s):	Iterations:	Time (s):	Iterations:
16	2	0.20	30	0.06	19	4.67	125	8.00E-6
16	3	0.22	34	0.07	23	5.54	127	1.60E-7
16	4	0.26	38	0.09	27	3.29	131	3.20E-9
16	5	0.28	42	0.10	31	2.98	129	6.40E-11

32	2	0.21	30	0.06	19	10.84	227	8.00E-6
32	3	0.24	34	0.07	23	12.61	229	1.60E-7
32	4	0.23	38	0.09	27	7.55	233	3.20E-9
32	5	0.25	42	0.10	31	6.57	238	6.40E-11

64	2	0.21	30	0.06	19	26.25	427	8.00E-6
64	3	0.24	34	0.08	23	29.16	429	1.60E-7
64	4	0.42	38	0.15	27	18.53	433	3.20E-9
64	5	0.30	42	0.10	31	15.01	433	6.40E-11

Bounded Retransmission Protocol

Contents

Introduction

Model Statistics

Model Construction Times

Model Checking

Case Studies

N:	MAX:	Time (s):
16	2	0.035
16	3	0.036
16	4	0.040
16	5	0.040

32	2	0.041
32	3	0.042
32	4	0.038
32	5	0.037

64	2	0.038
64	3	0.037
64	4	0.039
64	5	0.040