Related publications: [DKNP04, DKNP06]
Bluetooth is a short-range low-power open standard for implementing wireless personal area networks. To avoid potential problems of interference, it uses a frequency hopping scheme, where devices alternate rapidly in a pseudo-random fashion among agreed sets of frequencies. Before communication can take place, devices must undergo an initialisation process, organising themselves into small networks called piconets, comprising one master and up to 7 slave devices in which frequency hopping sequences are synchronised. The first step of this initialisation process is called device discovery or inquiry. During this, an inquiring device (which will become the master of a piconet) broadcasts messages to discover scanning devices in the vicinity (potential slave devices).
The following is a short description of the behaviour of inquiring and scanning devices according to the Bluetooth protocol. We work from the current version (1.2) of the Bluetooth Specification.
All Bluetooth devices use a 28 bit free-running clock which ticks in 312.5μs time-slots. Communicating devices use a previously agreed sequence of 32 frequencies which, for convenience, we refer simply to as 1,2,...,32.
On two consecutive 312.5μs time slots, the inquiring device broadcasts inquiry packets on two sequential frequencies. During the next two time slots, the device scans for a reply on these same two frequencies. It then moves on to the next two frequencies. This process continues until some specified bound on the number of replies received or the total time is exceeded.
The 32 frequencies used are split into two trains, A and B, of 16 frequencies each. The inquiring device swaps between trains, repeating each one 256 times (i.e. for 2.56 seconds). In addition, every 1.28 seconds, a frequency is swapped between train A and B. The resulting sequence of frequencies is shown below. Each line of the table is repeated 128 times, taking 1.28 seconds. Initially, train A (light grey) contains frequencies 1...16 and train B (dark grey) contains 17...32.
|
Scanning devices, i.e. those which wish to be discovered, listen on the same 32 frequencies, but hopping at a much slower speed to ensure eventual synchronisation. The devices alternate between a sleep state and a scan state. If, in the scan state, they successfully hear an inquiry packet, they wait 2 time slots and then send a reply packet. Subsequently, they performs a random back-off, waiting a random number of slots (0...127) before returning to the scan state. This is to prevent repeated collision of messages sent by two or more contending devices. In fact, the official Bluetooth specification permits a range of values for the maximum back-off. Our choice (127) is consistent with the other parameters we have adopted. Below is a summary of the behaviour and the time spent in each state.
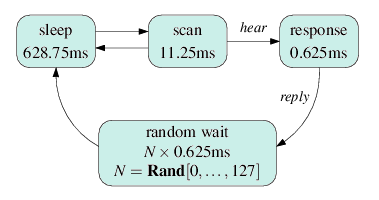
The frequency on which a device listens when it enters its scan state, known as its phase, cycles through the 32 frequencies in order according to the value of its clock and changes every 1.28 seconds.
We consider a single inquiring device and a single scanning device, which we refer to as the sender and receiver, respectively. Since the clocks of each device are digital (resolution 312.5μs) and drift can be assumed to be negligible over the (relative short) inquiry process, we model time elapsing in a synchronous fashion and our PRISM model is a DTMC.
A key modelling issue is the initial configuration of the model. We cannot assume that the sender and receiver both start in some fixed state because this is unrealistic. We restrict ourselves to the case where the sender is already transmitting inquiry packets and a receiver begins scanning after some unknown delay, which is a reasonable scenario. We can hence only fix the initial state of the receiver (variables r, freq and y) and also the counter rec. This gives a total of 17,179,869,184 possible initial states. For efficiency, we also fix the value of phase, and therefore must perform model checking on 32 separate DTMCs, each with 536,870,912 initial states.
In our model, the protocol ends when the sender has successfully received mrec replies from the receiver. For mrec=1, the average number of states in the 32 DTMCs was 3,440,187,794 and the PRISM MTBDD representation of it averaged at 13,713 nodes (267.8 KB). For mrec=2, the respective figures are 56,341,202,369 and 1,807,868 (35,310 KB).
The PRISM source code is given below.
// bluetooth model for one node in inquiry scan and one in inquiry // constants taken from standard // mxd/gxn/dxp 22/06/04 dtmc // removed time spent in sleep (turned into one big time transition) // and combined this with scan (only go to sleep if do not hear anything in scan) // also numbered frequencies from 1..16 and used extra variable to say what train // (i.e. 1..16 train 0 and 17..32 train 1) // PARAMETERS OF THE RECEIVER // scan window: time to scan a frequency 11.25ms [36 slots] // scan interval: time between scans 0.64 seconds (less than 1.28 so we can have a smaller random choice) [2048 slots] // phase - time until frequency changes 1.28 seconds (as specified in the standard) [4096 slots] //---------------------------------------------------------------------------------------------------------------------------- // CONSTANTS (from the standard) const int phase = 4096; // length of a phase (one frequency for the receiver) [1.28s] const int maxr = 127; // maximum random delay const int mrep = 128; // number of times a train is repeated before switching //---------------------------------------------------------------------------------------------------------------------------- // FORMULAE // we combine together scan and sleep when the receiver scans and hears nothing // the following formula is true in a state if and only if the receiver will hear something if it immediately starts scanning // (receiver scans for 32 slots so one loop of a train plus 4 more steps) formula success = // will see on current set of frequencies and there is time to complete a whole cycle ((rep<mrep & ((t1=((freq<=c)?train:1-train) & f1<=c) | (t1=((freq<=c)?1-train:train) & f1>c))) // will see on current set of frequencies and there is not time to complete a whole cycle | (rep=mrep & ((send=1 & freq<=f1) | (send>1 & freq<f1)) & ((t1=((freq<=c)?train:1-train) & f1<=c) | (t1=((freq<=c)?1-train:train) & f1>c))) // will see on next set of frequencies and at least a whole cycle to to | (rep=mrep-1 & c<16 & swap & ((t1=((freq<=c)?train:1-train) & f1<=c+1) | (t1=((freq<=c)?1-train:train) & f1>c+1)) & ((f1=1 & freq>=15) | (f1=2 & freq=16))) | (rep=mrep-1 & c<16 & !swap & ((t1=((freq<=c)?1-train:train) & f1<=c+1) | (t1=((freq<=c)?train:1-train) & f1>c+1)) & ((f1=1 & freq>=15) | (f1=2 & freq=16))) | (rep=mrep-1 & c=16 & (t1=((f1=1)?1-train:train)) & ((f1=1 & freq>=15) | (f1=2 & freq=16))) // will see on next set of frequencies and less than a whole cycle to do | (rep=mrep & c<16 & swap & ((t1=((freq<=c)?train:1-train) & f1<=c+1) | (t1=((freq<=c)?1-train:train) & f1>c+1)) & f1<=freq+2) | (rep=mrep & c<16 & !swap & ((t1=((freq<=c)?1-train:train) & f1<=c+1) | (t1=((freq<=c)?train:1-train) & f1>c+1)) & f1<=freq+2) | (rep=mrep & c=16 & (t1=((f1=1)?1-train:train)) & f1<=freq+2 & c=16)); // receiver swaps trains at end of sequence only when c is even formula swap = (((c=2)|(c=4)|(c=6)|(c=8)|(c=10)|(c=12)|(c=14)|(c=16))); // receiver swaps trains when changing frequency set (when receiver sleeps) formula swap2 = ((((c=2)|(c=4)|(c=6)|(c=8)|(c=10)|(c=12)|(c=14))) & freq=c+1) | (c=16 & freq=1) | ((((c=1)|(c=3)|(c=5)|(c=7)|(c=9)|(c=11)|(c=13)|(c=15))) & freq!=c+1); // state where receiver's next time step corresponds to the whole of scan and sleep (scan interval) formula sleep = (receiver=0 & y1=1); // when the receiver hears something formula hear = (freq1=freq & train1=train & send=1); //---------------------------------------------------------------------------------------------------------------------------- // module for first receiver module receiver1 y1 : [0..2*maxr+1]; //clock of the receiver receiver : [0..3]; // 0 - next state scan // 1 listeninging on frequencies // 2 sending and computing the random delay // 3 wait random delay freq1 : [0..16]; // frequency of the receiver (use 0 for no frequency set) train1 : [0..1]; // train of the receiver [time] receiver=0 & y1=1 -> (y1'=y1-1); // time passes (2048 time slots pass) [] receiver=0 & y1=0 & success -> (receiver'=1) & (freq1'=f1) & (train1'=t1); // move to scan [] receiver=0 & y1=0 & !success -> (receiver'=0) & (y1'=1); // will not hear anything so scan then sleep // scanning (will hear something - unless I have done something wrong) [time] receiver=1 & !hear -> (y1'=y1); // hear nothing: stay in scan and let 1 slot pass [] receiver=1 & hear -> (receiver'=2) & (y1'=2) & (freq1'=0) & (train1'=0); // hear something: get ready to send reply and let time pass // replying [time] receiver=2 & y1>0 -> (y1'=y1-1); // let time pass (1 slot) [reply] receiver=2 & y1=0 -> 1/(maxr+1) : (receiver'=3) & (y1'=0) // reply and make random choice + 1/(maxr+1) : (receiver'=3) & (y1'=2*1) + 1/(maxr+1) : (receiver'=3) & (y1'=2*2) + 1/(maxr+1) : (receiver'=3) & (y1'=2*3) + 1/(maxr+1) : (receiver'=3) & (y1'=2*4) + 1/(maxr+1) : (receiver'=3) & (y1'=2*5) + 1/(maxr+1) : (receiver'=3) & (y1'=2*6) + 1/(maxr+1) : (receiver'=3) & (y1'=2*7) + 1/(maxr+1) : (receiver'=3) & (y1'=2*8) + 1/(maxr+1) : (receiver'=3) & (y1'=2*9) + 1/(maxr+1) : (receiver'=3) & (y1'=2*10) + 1/(maxr+1) : (receiver'=3) & (y1'=2*11) + 1/(maxr+1) : (receiver'=3) & (y1'=2*12) + 1/(maxr+1) : (receiver'=3) & (y1'=2*13) + 1/(maxr+1) : (receiver'=3) & (y1'=2*14) + 1/(maxr+1) : (receiver'=3) & (y1'=2*15) + 1/(maxr+1) : (receiver'=3) & (y1'=2*16) + 1/(maxr+1) : (receiver'=3) & (y1'=2*17) + 1/(maxr+1) : (receiver'=3) & (y1'=2*18) + 1/(maxr+1) : (receiver'=3) & (y1'=2*19) + 1/(maxr+1) : (receiver'=3) & (y1'=2*20) + 1/(maxr+1) : (receiver'=3) & (y1'=2*21) + 1/(maxr+1) : (receiver'=3) & (y1'=2*22) + 1/(maxr+1) : (receiver'=3) & (y1'=2*23) + 1/(maxr+1) : (receiver'=3) & (y1'=2*24) + 1/(maxr+1) : (receiver'=3) & (y1'=2*25) + 1/(maxr+1) : (receiver'=3) & (y1'=2*26) + 1/(maxr+1) : (receiver'=3) & (y1'=2*27) + 1/(maxr+1) : (receiver'=3) & (y1'=2*28) + 1/(maxr+1) : (receiver'=3) & (y1'=2*29) + 1/(maxr+1) : (receiver'=3) & (y1'=2*30) + 1/(maxr+1) : (receiver'=3) & (y1'=2*31) + 1/(maxr+1) : (receiver'=3) & (y1'=2*32) + 1/(maxr+1) : (receiver'=3) & (y1'=2*33) + 1/(maxr+1) : (receiver'=3) & (y1'=2*34) + 1/(maxr+1) : (receiver'=3) & (y1'=2*35) + 1/(maxr+1) : (receiver'=3) & (y1'=2*36) + 1/(maxr+1) : (receiver'=3) & (y1'=2*37) + 1/(maxr+1) : (receiver'=3) & (y1'=2*38) + 1/(maxr+1) : (receiver'=3) & (y1'=2*39) + 1/(maxr+1) : (receiver'=3) & (y1'=2*40) + 1/(maxr+1) : (receiver'=3) & (y1'=2*41) + 1/(maxr+1) : (receiver'=3) & (y1'=2*42) + 1/(maxr+1) : (receiver'=3) & (y1'=2*43) + 1/(maxr+1) : (receiver'=3) & (y1'=2*44) + 1/(maxr+1) : (receiver'=3) & (y1'=2*45) + 1/(maxr+1) : (receiver'=3) & (y1'=2*46) + 1/(maxr+1) : (receiver'=3) & (y1'=2*47) + 1/(maxr+1) : (receiver'=3) & (y1'=2*48) + 1/(maxr+1) : (receiver'=3) & (y1'=2*49) + 1/(maxr+1) : (receiver'=3) & (y1'=2*50) + 1/(maxr+1) : (receiver'=3) & (y1'=2*51) + 1/(maxr+1) : (receiver'=3) & (y1'=2*52) + 1/(maxr+1) : (receiver'=3) & (y1'=2*53) + 1/(maxr+1) : (receiver'=3) & (y1'=2*54) + 1/(maxr+1) : (receiver'=3) & (y1'=2*55) + 1/(maxr+1) : (receiver'=3) & (y1'=2*56) + 1/(maxr+1) : (receiver'=3) & (y1'=2*57) + 1/(maxr+1) : (receiver'=3) & (y1'=2*58) + 1/(maxr+1) : (receiver'=3) & (y1'=2*59) + 1/(maxr+1) : (receiver'=3) & (y1'=2*60) + 1/(maxr+1) : (receiver'=3) & (y1'=2*61) + 1/(maxr+1) : (receiver'=3) & (y1'=2*62) + 1/(maxr+1) : (receiver'=3) & (y1'=2*63) + 1/(maxr+1) : (receiver'=3) & (y1'=2*64) + 1/(maxr+1) : (receiver'=3) & (y1'=2*65) + 1/(maxr+1) : (receiver'=3) & (y1'=2*66) + 1/(maxr+1) : (receiver'=3) & (y1'=2*67) + 1/(maxr+1) : (receiver'=3) & (y1'=2*68) + 1/(maxr+1) : (receiver'=3) & (y1'=2*69) + 1/(maxr+1) : (receiver'=3) & (y1'=2*70) + 1/(maxr+1) : (receiver'=3) & (y1'=2*71) + 1/(maxr+1) : (receiver'=3) & (y1'=2*72) + 1/(maxr+1) : (receiver'=3) & (y1'=2*73) + 1/(maxr+1) : (receiver'=3) & (y1'=2*74) + 1/(maxr+1) : (receiver'=3) & (y1'=2*75) + 1/(maxr+1) : (receiver'=3) & (y1'=2*76) + 1/(maxr+1) : (receiver'=3) & (y1'=2*77) + 1/(maxr+1) : (receiver'=3) & (y1'=2*78) + 1/(maxr+1) : (receiver'=3) & (y1'=2*79) + 1/(maxr+1) : (receiver'=3) & (y1'=2*80) + 1/(maxr+1) : (receiver'=3) & (y1'=2*81) + 1/(maxr+1) : (receiver'=3) & (y1'=2*82) + 1/(maxr+1) : (receiver'=3) & (y1'=2*83) + 1/(maxr+1) : (receiver'=3) & (y1'=2*84) + 1/(maxr+1) : (receiver'=3) & (y1'=2*85) + 1/(maxr+1) : (receiver'=3) & (y1'=2*86) + 1/(maxr+1) : (receiver'=3) & (y1'=2*87) + 1/(maxr+1) : (receiver'=3) & (y1'=2*88) + 1/(maxr+1) : (receiver'=3) & (y1'=2*89) + 1/(maxr+1) : (receiver'=3) & (y1'=2*90) + 1/(maxr+1) : (receiver'=3) & (y1'=2*91) + 1/(maxr+1) : (receiver'=3) & (y1'=2*92) + 1/(maxr+1) : (receiver'=3) & (y1'=2*93) + 1/(maxr+1) : (receiver'=3) & (y1'=2*94) + 1/(maxr+1) : (receiver'=3) & (y1'=2*95) + 1/(maxr+1) : (receiver'=3) & (y1'=2*96) + 1/(maxr+1) : (receiver'=3) & (y1'=2*97) + 1/(maxr+1) : (receiver'=3) & (y1'=2*98) + 1/(maxr+1) : (receiver'=3) & (y1'=2*99) + 1/(maxr+1) : (receiver'=3) & (y1'=2*100) + 1/(maxr+1) : (receiver'=3) & (y1'=2*101) + 1/(maxr+1) : (receiver'=3) & (y1'=2*102) + 1/(maxr+1) : (receiver'=3) & (y1'=2*103) + 1/(maxr+1) : (receiver'=3) & (y1'=2*104) + 1/(maxr+1) : (receiver'=3) & (y1'=2*105) + 1/(maxr+1) : (receiver'=3) & (y1'=2*106) + 1/(maxr+1) : (receiver'=3) & (y1'=2*107) + 1/(maxr+1) : (receiver'=3) & (y1'=2*108) + 1/(maxr+1) : (receiver'=3) & (y1'=2*109) + 1/(maxr+1) : (receiver'=3) & (y1'=2*110) + 1/(maxr+1) : (receiver'=3) & (y1'=2*111) + 1/(maxr+1) : (receiver'=3) & (y1'=2*112) + 1/(maxr+1) : (receiver'=3) & (y1'=2*113) + 1/(maxr+1) : (receiver'=3) & (y1'=2*114) + 1/(maxr+1) : (receiver'=3) & (y1'=2*115) + 1/(maxr+1) : (receiver'=3) & (y1'=2*116) + 1/(maxr+1) : (receiver'=3) & (y1'=2*117) + 1/(maxr+1) : (receiver'=3) & (y1'=2*118) + 1/(maxr+1) : (receiver'=3) & (y1'=2*119) + 1/(maxr+1) : (receiver'=3) & (y1'=2*120) + 1/(maxr+1) : (receiver'=3) & (y1'=2*121) + 1/(maxr+1) : (receiver'=3) & (y1'=2*122) + 1/(maxr+1) : (receiver'=3) & (y1'=2*123) + 1/(maxr+1) : (receiver'=3) & (y1'=2*124) + 1/(maxr+1) : (receiver'=3) & (y1'=2*125) + 1/(maxr+1) : (receiver'=3) & (y1'=2*126) + 1/(maxr+1) : (receiver'=3) & (y1'=2*127); // waiting random delay [time] receiver=3 & y1>0 -> (y1'=y1-1); // let time pass (1 slot) // finished waiting random delay (listen again) [] receiver=3 & y1=0 & success -> (receiver'=1) & (freq1'=f1) & (train1'=t1); // move to scan [] receiver=3 & y1=0 & !success -> (receiver'=0) & (y1'=1); // will not hear anything (combine scan and sleep) endmodule //---------------------------------------------------------------------------------------------------------------------------- // frequency for first receiver module frequency1 z1 : [1..phase];// clock for phase f1 : [1..16]; // frequency of receiver t1 : [0..1]; // train of receiver // update frequency (1 slot passes) [time] !sleep & z1<phase -> (z1'=z1+1); [time] !sleep & z1=phase & f1<16 -> (z1'=1) & (f1'=f1+1); [time] !sleep & z1=phase & f1=16 -> (z1'=1) & (f1'=1) & (t1'=1-t1); // update frequency (2048 slots pass) [time] sleep & z1<=2048 -> (z1'=z1+2048); [time] sleep & z1>2048 & f1<16 -> (z1'=z1-2048) & (f1'=f1+1); [time] sleep & z1>2048 & f1=16 -> (z1'=z1-2048) & (f1'=1) & (t1'=1-t1); // update frequency: something is sent by the receiver (cannot be sleeping here) [reply] true -> (f1'=(f1<16)?f1+1:1) & (t1'=(f1<16)?t1:1-t1); endmodule //---------------------------------------------------------------------------------------------------------------------------- // sender // note to make things easier we do not change the frequency for receiving // will only work if the delays are divisible by 4 otherwise it will cause problems // frequency of sender module sender // still should try some different orderings? send : [1..3]; // 1 sending and 2,3 receiving freq : [1..16]; // current frequency mod 16 freq+train*16 train : [0..1]; // used to work out the frequency (actual frequency equals freq+train*16) c : [1..16]; // used to work out the trains rep : [1..mrep]; // no of repetitions of a train // sending [time] !sleep & send=1 & (((freq=1)|(freq=3)|(freq=5)|(freq=7)|(freq=9)|(freq=11)|(freq=13)|(freq=15))) & freq!=c -> (freq'=freq+1); [time] !sleep & send=1 & (((freq=1)|(freq=3)|(freq=5)|(freq=7)|(freq=9)|(freq=11)|(freq=13)|(freq=15))) & freq=c -> (freq'=freq+1) & (train'=1-train); [time] !sleep & send=1 & (((freq=2)|(freq=4)|(freq=6)|(freq=8)|(freq=10)|(freq=12)|(freq=14)|(freq=16))) -> (send'=2); // receiving [time] !sleep & send=2 -> (send'=3); [time] !sleep & send=3 & freq<16 & freq!=c -> (send'=1) & (freq'=freq+1); [time] !sleep & send=3 & freq<16 & freq=c -> (send'=1) & (freq'=freq+1) & (train'=1-train); [time] !sleep & send=3 & freq=16 & rep<mrep & c!=16 -> (send'=1) & (freq'=1) & (train'=1-train) & (rep'=rep+1); [time] !sleep & send=3 & freq=16 & rep<mrep & c=16 -> (send'=1) & (freq'=1) & (rep'=rep+1); [time] !sleep & send=3 & freq=16 & rep=mrep -> (send'=1) & (freq'=1) & (train'=swap?1-train:train) & (c'=c=16?1:c+1) & (rep'=1); // big time step (2048 slots = 64 repetitions) [time] sleep & rep<=64 -> (rep'=rep+64); // sleeping does not change frequency set [time] sleep & rep>64 -> (rep'=rep-64) & (c'=c=16?1:c+1) & (train'=swap2?1-train:train); // sleeping changes current frequency set endmodule //---------------------------------------------------------------------------------------------------------------------------- const int mrec; // after receiving mrec messages the inquiry is stopped // counts the number of replies received module replies // no of non garbled received messages rec : [0..mrec]; [time] rec<mrec -> (rec'=rec); [reply] rec<mrec -> (rec'=min(rec+1,mrec)); [] rec=mrec -> (rec'=rec); endmodule //---------------------------------------------------------------------------------------------------------------------------- // specify initial state (only that receiver starts scanning and nothing sent) // note as changed the sender so that for freq to be odd send must equal 1 we need the extra condition // init rec=0 & y1=0 & receiver=0 & freq1=0 & train1=0 & (send=1 | freq=2,4,6,8,10,12,14,16) endinit const int k; // frequency the sender starts on const int T; // train that the sender starts on init receiver=0 & y1=0 & freq1=0 & train1=0 & // initial state of the receiver rec=0 & // nothing received yet f1=k & t1=T & // initial frequency of the receiver (based on its clock) (send=1 |((freq=2)|(freq=4)|(freq=6)|(freq=8)|(freq=10)|(freq=12)|(freq=14)|(freq=16))) // condition required on the sender endinit //---------------------------------------------------------------------------------------------------------------------------- // rewards - to compute expected time rewards "time" [time] !(receiver=0 & y1=1) : 1; [time] receiver=0 & y1=1 : 2048; endrewards
We compute the expected time for completion of the inquiry process, i.e. the time elapsed until the bound mrec on the number of replies heard by the sender has been met. We compute this for all 17,179,869,184 possible initial states.
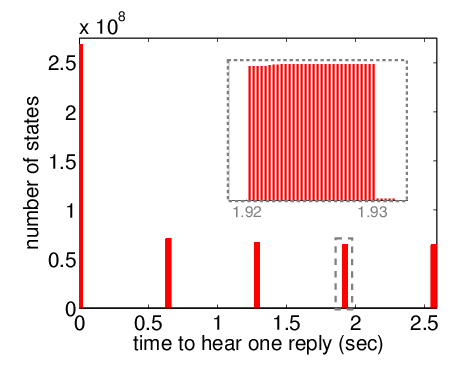
For mrec=1, the best- and worst-case expected times are 635μs (2 slots) and 2.5716s (8,229 slots), respectively. Below is a plot of the expected time against the number of initial states which result in this time. The discontinuities (an example is highlighted in the inset) correspond to the cases where the receiver sleeps different numbers of times before successfully hearing an inquiry packet. The 5 peaks correspond to 0,1,2,3 and 4 sleeps.
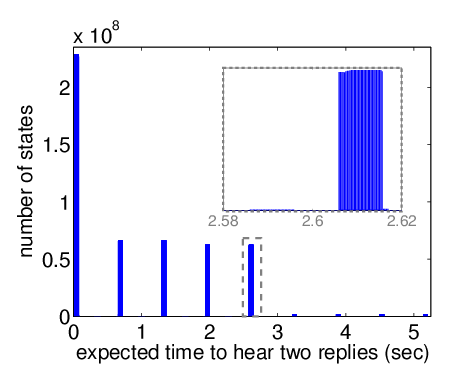
For mrec=2, the best- and worst-case expected times are 0.0456s (146.0 slots) and 5.1569 seconds 5.177 seconds (16,565 slots), respectively. Again, we plot the expected time against the number of initial states which result in this time. Here, there are 9 peaks (of which 4 are much smaller) corresponding to the receiver sleeping 0,1,...,8 times before hearing a message.
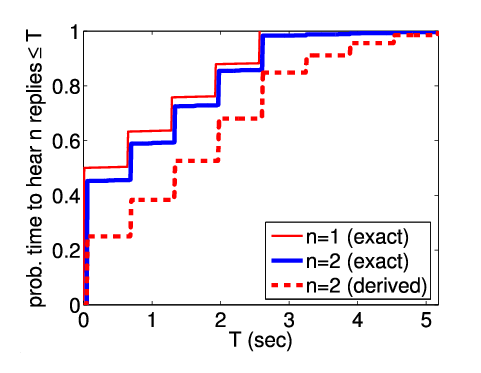
By assuming that there is a uniform distribution on the set of possible initial configurations, we can calculate the cumulative probability distribution function for the time that it takes the sender to hear either one or two replies. This is shown in the graph below. In addition, we compare the function for two replies to a derived cumulative probability distribution function, based on the additional assumption that the times to hear each of the two messages are independent. This is constructed as a convolution of two copies of the distribution plotted for the case mrec=1 together with a distribution representing the random delay made by the receiver between sending the first reply and beginning its next scan. Clearly, we see that any analysis based on such an assumption is flawed and results in incorrect results. We illustrate that, if the receiver sleeps before sending its first reply, it is less likely to sleep the second time.
Finally, we extract from the three cumulative probability distributions we have presented above, the probability that the receiver sleeps at most K times before sending its first reply to the sender. These are shown in the table below.
| K: | Probability: | ||||
| mrec=1 | mrec=1 (v.1.1) | mrec=2 (exact) | mrec=2 (derived) | ||
| 0 | 0.500305 | 0.461240 | 0.455377 | 0.250305 | |
| 1 | 0.633575 | 0.596265 | 0.591388 | 0.383657 | |
| 2 | 0.759062 | 0.731585 | 0.729611 | 0.526981 | |
| 3 | 0.879674 | 0.857913 | 0.855804 | 0.681114 | |
| 4 | 1 | 0.984295 | 0.984253 | 0.849408 | |
| 5 | 1 | 0.988269 | 0.988328 | 0.911750 | |
| 6 | 1 | 0.992398 | 0.992546 | 0.956496 | |
| 7 | 1 | 0.996294 | 0.996534 | 0.985521 | |
| 8 | 1 | 1 | 1 | 1 | |
We also include in this table results from an additional verification we have performed, on a model of the previous version (1.1) of the Bluetooth specification (our analysis uses the current version 1.2). The main difference is that, in version 1.1, the receiver only sends a reply to every second message received. We were able to modify our PRISM model to reflect this change and rerun our experiments. Above, we successfully illustrate that, as was intended, version 1.2 indeed results in improved expected times.