(Itai & Rodeh)
This case study is based on the asynchronous leader election protocol of Itai & Rodeh [IR90]. This protocol solves the following problem.
| Given an asynchronous ring of N processors design a protocol such that they will be able to elect a leader (a uniquely designated processor) by sending messages around the ring. |
The protocol begins with all processors active. Each active process performs the following steps until it becomes inactive (when processors become inactive they only relay messages received):
| 1. | Choose 0 or 1 each with probability 0.5, and send the choice to the next processor. |
| 2. | If the processor chose 0 and the active processor preceding it in the ring chose 1 become inactive. |
| 3. | Send a counter around the ring to check whether it is the only active processor. If it is the only active processor then become leader, else repeat. |
We assume that the ring is asynchronous: each processor has its own clock which has no relation to that of the other processors. Therefore, we cannot say that a message a processor wants to send will arrive at its destination processor at the same time slot. Instead, we assume that the order of the arrival of messages is governed by a scheduler which determines which message is sent next.
By way of example, the PRISM source code for the case where N=4 is given below.
// asynchronous leader election // 4 processes // gxn/dxp 29/01/01 mdp const N=4; // number of processes module process1 // COUNTER c1 : [0..N-1]; // STATES s1 : [0..4]; // 0 make choice // 1 have not received neighbours choice // 2 active // 3 inactive // 4 leader // PREFERENCE p1 : [0..1]; // VARIABLES FOR SENDING AND RECEIVING receive1 : [0..2]; // not received anything // received choice // received counter sent1 : [0..2]; // not send anything // sent choice // sent counter // pick value [] (s1=0) -> 0.5 : (s1'=1) & (p1'=0) + 0.5 : (s1'=1) & (p1'=1); // send preference [p12] (s1=1) & (sent1=0) -> (sent1'=1); // receive preference // stay active [p41] (s1=1) & (receive1=0) & !( (p1=0) & (p4=1) ) -> (s1'=2) & (receive1'=1); // become inactive [p41] (s1=1) & (receive1=0) & (p1=0) & (p4=1) -> (s1'=3) & (receive1'=1); // send preference (can now reset preference) [p12] (s1=2) & (sent1=0) -> (sent1'=1) & (p1'=0); // send counter (already sent preference) // not received counter yet [c12] (s1=2) & (sent1=1) & (receive1=1) -> (sent1'=2); // received counter (pick again) [c12] (s1=2) & (sent1=1) & (receive1=2) -> (s1'=0) & (p1'=0) & (c1'=0) & (sent1'=0) & (receive1'=0); // receive counter and not sent yet (note in this case do not pass it on as will send own counter) [c41] (s1=2) & (receive1=1) & (sent1<2) -> (receive1'=2); // receive counter and sent counter // only active process (decide) [c41] (s1=2) & (receive1=1) & (sent1=2) & (c4=N-1) -> (s1'=4) & (p1'=0) & (c1'=0) & (sent1'=0) & (receive1'=0); // other active process (pick again) [c41] (s1=2) & (receive1=1) & (sent1=2) & (c4<N-1) -> (s1'=0) & (p1'=0) & (c1'=0) & (sent1'=0) & (receive1'=0); // send preference (must have received preference) and can now reset [p12] (s1=3) & (receive1>0) & (sent1=0) -> (sent1'=1) & (p1'=0); // send counter (must have received counter first) and can now reset [c12] (s1=3) & (receive1=2) & (sent1=1) -> (s1'=3) & (p1'=0) & (c1'=0) & (sent1'=0) & (receive1'=0); // receive preference [p41] (s1=3) & (receive1=0) -> (p1'=p4) & (receive1'=1); // receive counter [c41] (s1=3) & (receive1=1) & (c4<N-1) -> (c1'=c4+1) & (receive1'=2); // done [done] (s1=4) -> (s1'=s1); // add loop for processes who are inactive [done] (s1=3) -> (s1'=s1); endmodule module process2=process1[s1=s2,p1=p2,c1=c2,sent1=sent2,receive1=receive2,p12=p23,p41=p12,c12=c23,c41=c12,p4=p1,c4=c1] endmodule module process3=process1[s1=s3,p1=p3,c1=c3,sent1=sent3,receive1=receive3,p12=p34,p41=p23,c12=c34,c41=c23,p4=p2,c4=c2] endmodule module process4=process1[s1=s4,p1=p4,c1=c4,sent1=sent4,receive1=receive4,p12=p41,p41=p34,c12=c41,c41=c34,p4=p3,c4=c3] endmodule // reward - expected number of rounds (equals the number of times a process receives a counter) rewards "rounds" [c12] true : 1; endrewards
The table below shows statistics for the MDPs we have built for different values of the constants N and K. The tables include:
| N: | Model: | MTBDD: | Construction: | ||||||
| States: | Transitions: | Nodes: | Leaves: | Time (s): | Iter.s: | ||||
| 3 | 364 | 654 | 3,345 | 3 | 0.146 | 18 | |||
| 4 | 3,172 | 7,144 | 10,747 | 3 | 0.341 | 31 | |||
| 5 | 27,299 | 74,365 | 31,414 | 3 | 1.407 | 42 | |||
| 6 | 237,656 | 760,878 | 77,980 | 3 | 5.664 | 61 | |||
| 7 | 2,095,783 | 7,714,385 | 180,361 | 3 | 20.91 | 77 | |||
| 8 | 18,674,484 | 77,708,080 | 392,068 | 3 | 79.37 | 94 | |||
In this case study we use the BDD based fixpoint algorithmProb0E, which find those states for which the maximum probability of satisfying the formula is greater than 0. When model checking, we have the following requirement:
Scheduler-Liveness: for each time t and any processor i, there exists a time t' > t in which i is scheduled.
This corresponds to the conditions on the adversary/scheduler which we impose by model checking against only fair adversaries.
We have model checked the following properties:
Only one leader is elected.
This is an invariance property and in the case of 4 processes corresponds to the PCTL formula:
Model checking times:
| N: | Time (s): | |
| 3 | 0.009 | |
| 4 | 0.010 | |
| 5 | 0.010 | |
| 6 | 0.021 | |
| 7 | 0.039 | |
| 8 | 0.148 |
With probability 1, eventually a leader is elected.
In the case of 4 processes this property can be expressed in PCTL as follows:
Model checking times:
| N: | Prob0E precomputation: | ||
| Time (s): | Iterations: | ||
| 3 | 0.076 | 24 | |
| 4 | 0.53 | 33 | |
| 5 | 3.02 | 51 | |
| 6 | 13.8 | 62 | |
| 7 | 55.5 | 76 | |
| 8 | 198 | 90 | |
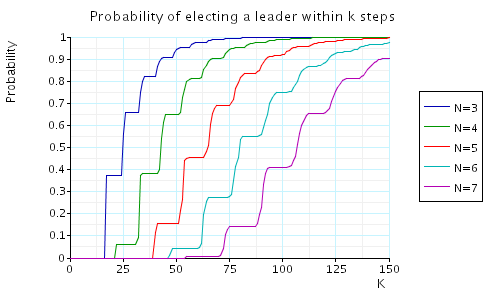
The minimum/maximum probability of electing a leader within k steps.
For the case of 4 processes these property can be expressed in PCTL as follows:
In the graph below we have plotted these probabilities as the number of processes varies. Note that the minimum and maximum probabilities are the same in each case.
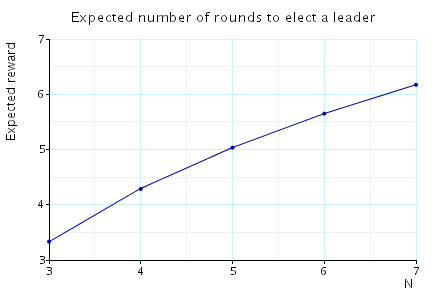
The minimum/maximum expected number of rounds to elect a leader.
For the case of 4 processes these property can be expressed in PCTL as follows:
In the graph below we have plotted these expected values as the number of processes varies. Note that the minimum and maximum expected time are the same in each case.